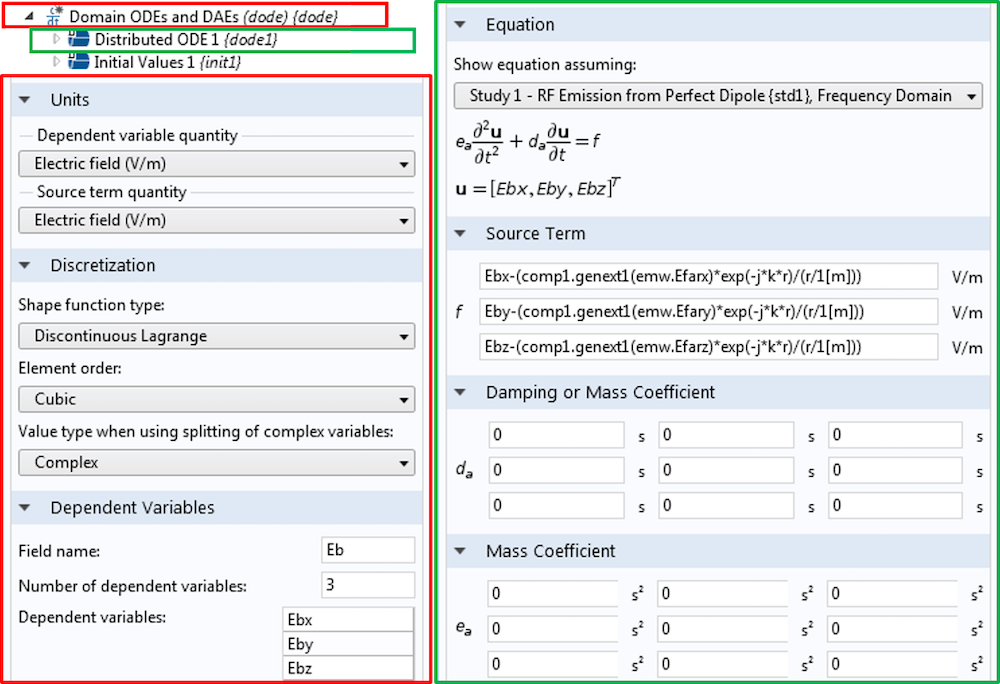
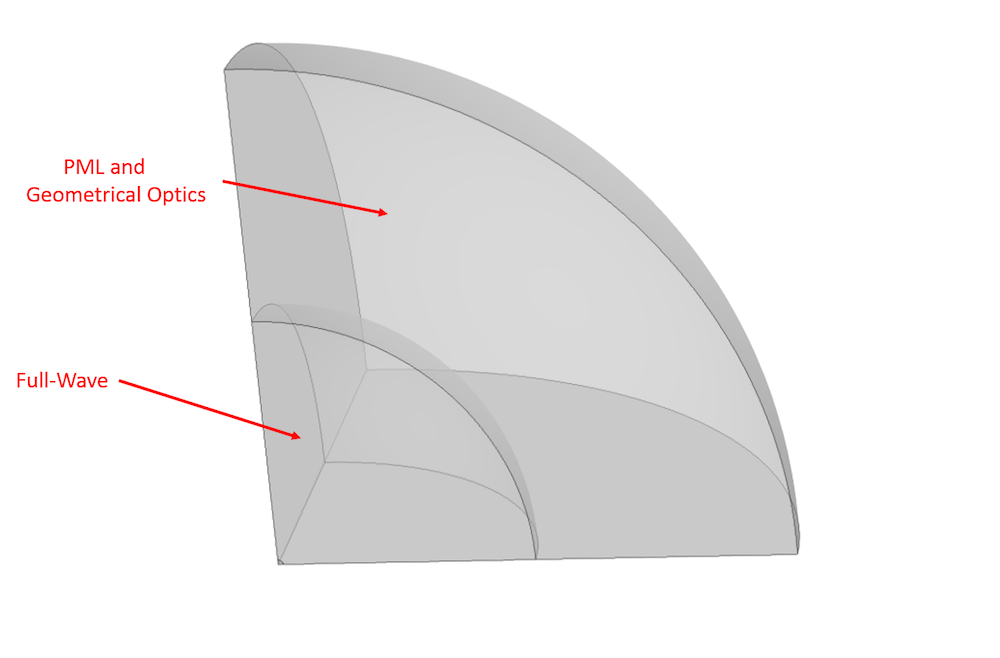
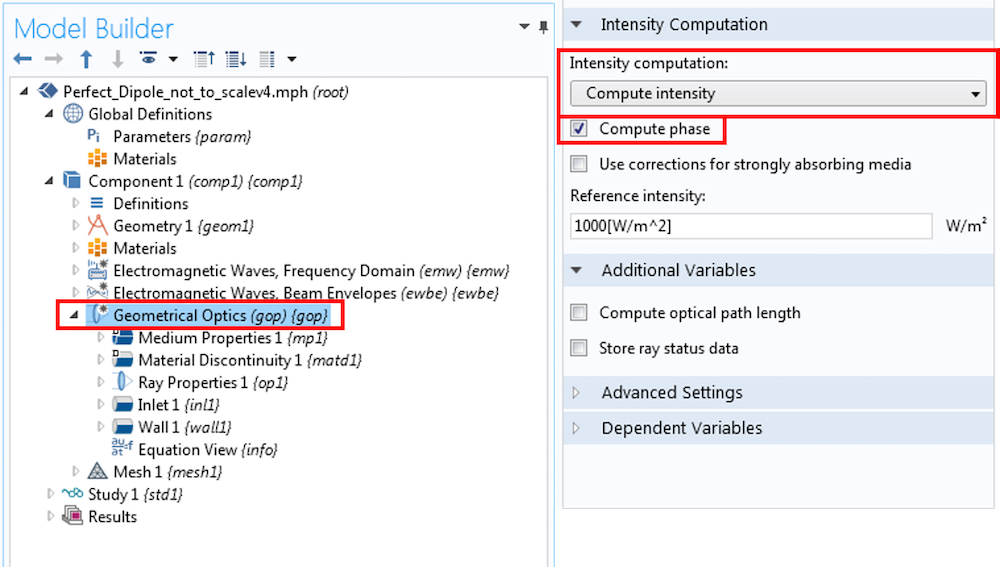
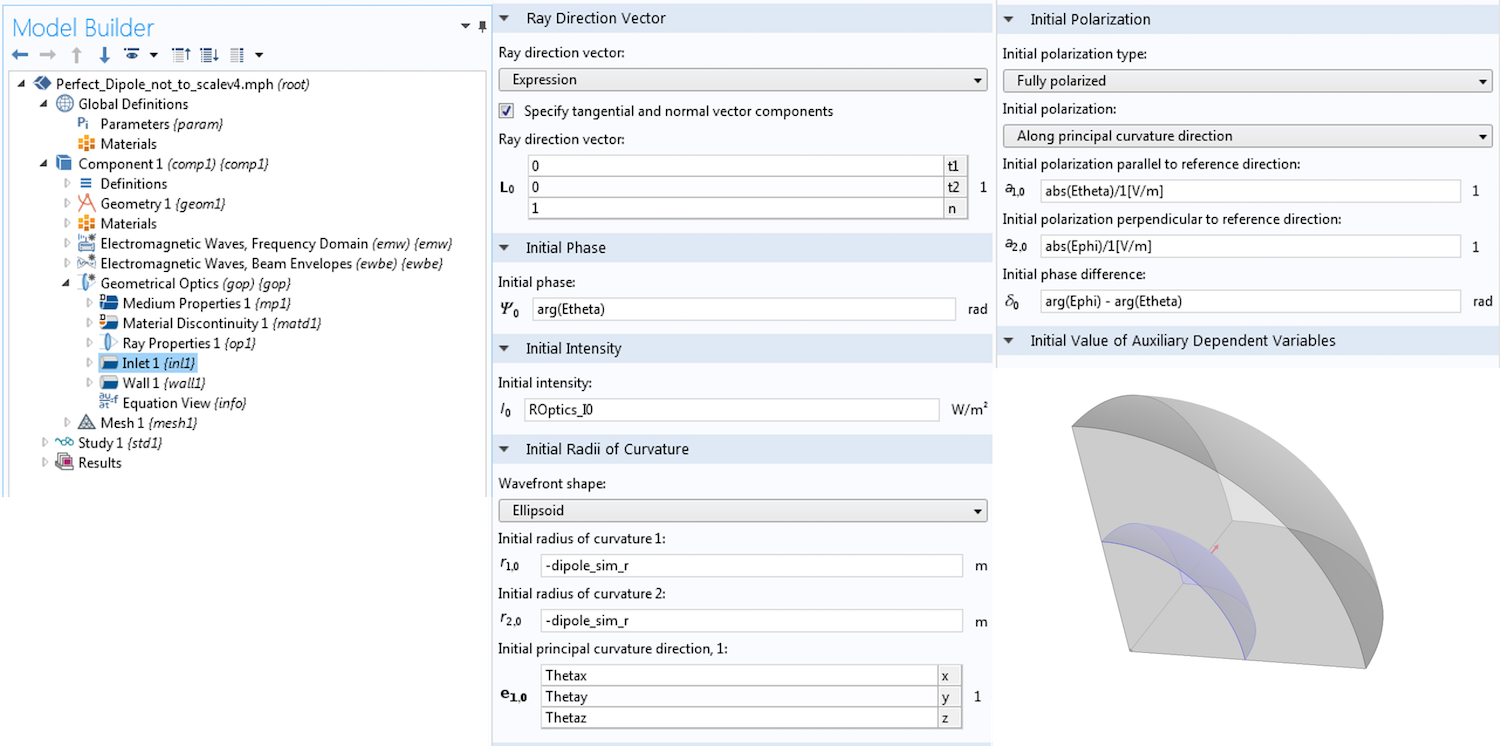
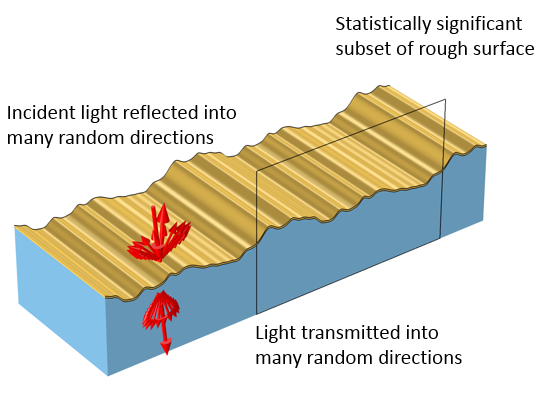
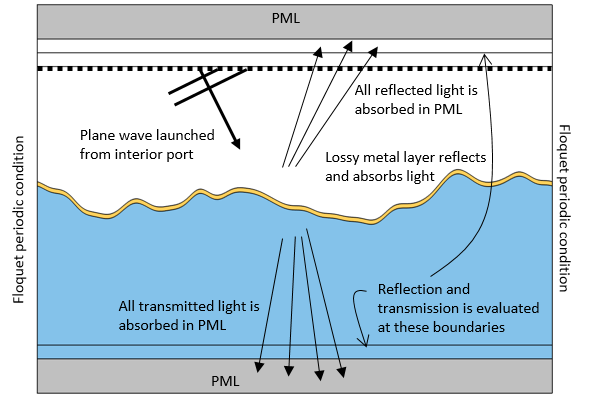
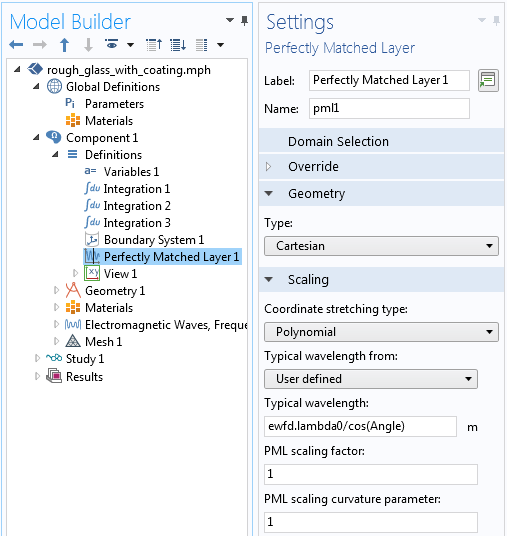
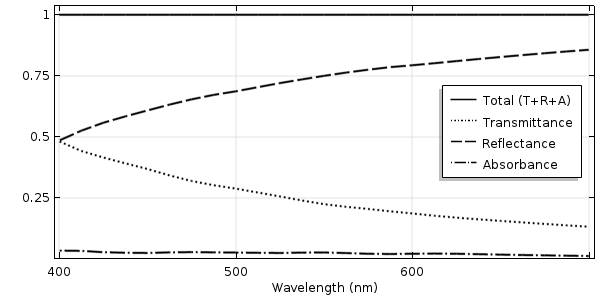
The Gaussian beam is recognized as one of the most useful light sources. To describe the Gaussian beam, there is a mathematical formula called the paraxial Gaussian beam formula. Today, we’ll learn about this formula, including its limitations, by using the Electromagnetic Waves, Frequency Domain interface in the COMSOL Multiphysics® software. We’ll also provide further detail into a potential cause of error when utilizing this formula. In a later blog post, we’ll provide solutions to the limitations discussed here.

Gaussian Beam: The Most Useful Light Source and Its Formula

Because they can be focused to the smallest spot size of all electromagnetic beams, Gaussian beams can deliver the highest resolution for imaging, as well as the highest power density for a fixed incident power, which can be important in fields such as material processing. These qualities are why lasers are such attractive light sources. To obtain the tightest possible focus, most commercial lasers are designed to operate in the lowest transverse mode, called the Gaussian beam.

As such, it would be reasonable to want to simulate a Gaussian beam with the smallest spot size. There is a formula that predicts real Gaussian beams in experiments very well and is convenient to apply in simulation studies. However, there is a limitation attributed to using this formula. The limitation appears when you are trying to describe a Gaussian beam with a spot size near its wavelength. In other words, the formula becomes less accurate when trying to observe the most beneficial feature of the Gaussian beam in simulation. In a future blog post, we will discuss ways to simulate Gaussian beams more accurately; for the remainder of this post, we will focus exclusively on the paraxial Gaussian beam.

A schematic illustrating the converging, focusing, and diverging of a Gaussian beam.

Note: The term “Gaussian beam” can sometimes be used to describe a beam with a “Gaussian profile” or “Gaussian distribution”. When we use the term “Gaussian beam” here, it always means a “focusing” or “propagating” Gaussian beam, which includes the amplitude and the phase.

Deriving the Paraxial Gaussian Beam Formula

The paraxial Gaussian beam formula is an approximation to the Helmholtz equation derived from Maxwell’s equations. This is the first important element to note, while the other portions of our discussion will focus on how the formula is derived and what types of assumptions are made from it.

Because the laser beam is an electromagnetic beam, it satisfies the Maxwell equations. The time-harmonic assumption (the wave oscillates at a single frequency in time) changes the Maxwell equations to the frequency domain from the time domain, resulting in the monochromatic (single wavelength) Helmholtz equation. Assuming a certain polarization, it further reduces to a scalar Helmholtz equation, which is written in 2D for the out-of-plane electric field for simplicity:

where for wavelength in vacuum.

The original idea of the paraxial Gaussian beam starts with approximating the scalar Helmholtz equation by factoring out the propagating factor and leaving the slowly varying function, i.e., , where the propagation axis is in and is the slowly varying function. This will yield an identity

This factorization is reasonable for a wave in a laser cavity propagating along the optical axis. The next assumption is that , which means that the envelope of the propagating wave is slow along the optical axis, and , which means that the variation of the wave in the optical axis is slower than that in the transverse axis. These assumptions derive an approximation to the Helmholtz equation, which is called the paraxial Helmholtz equation, i.e.,

The special solution to this paraxial Helmholtz equation gives the paraxial Gaussian beam formula. For a given waist radius at the focus point, the slowly varying function is given by

where , , and are the beam radius as a function of , the radius of curvature of the wavefront, and the Gouy phase, respectively. The following definitions apply: , , , and .

Here, is referred to as the Rayleigh range. Outside of the Rayleigh range, the Gaussian beam size becomes proportional to the distance from the focal point and the intensity position diverges at an approximate divergence angle of .

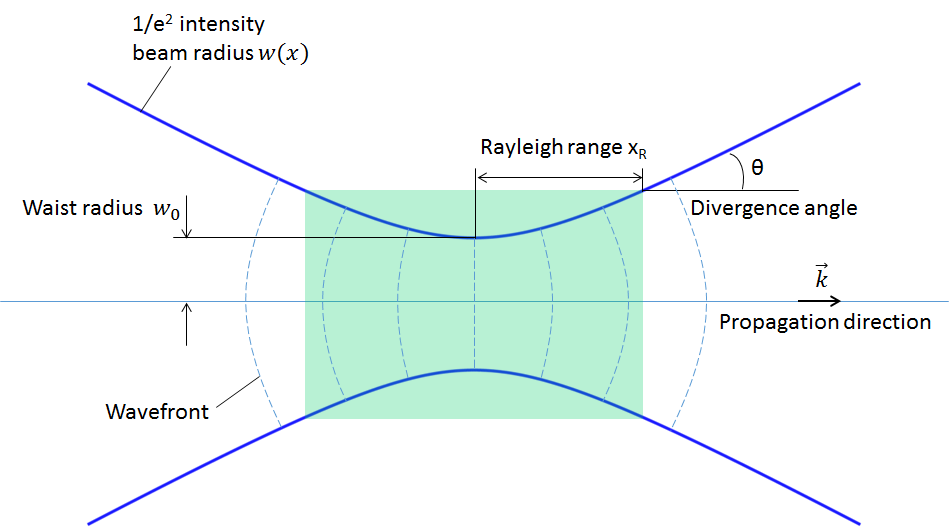
Definition of the paraxial Gaussian beam.

Note: It is important to be clear about which quantities are given and which ones are being calculated. To specify a paraxial Gaussian beam, either the waist radius or the far-field divergence angle must be given. These two quantities are dependent on each other through the approximate divergence angle equation. All other quantities and functions are derived from and defined by these quantities.

Simulating Paraxial Gaussian Beams in COMSOL Multiphysics®

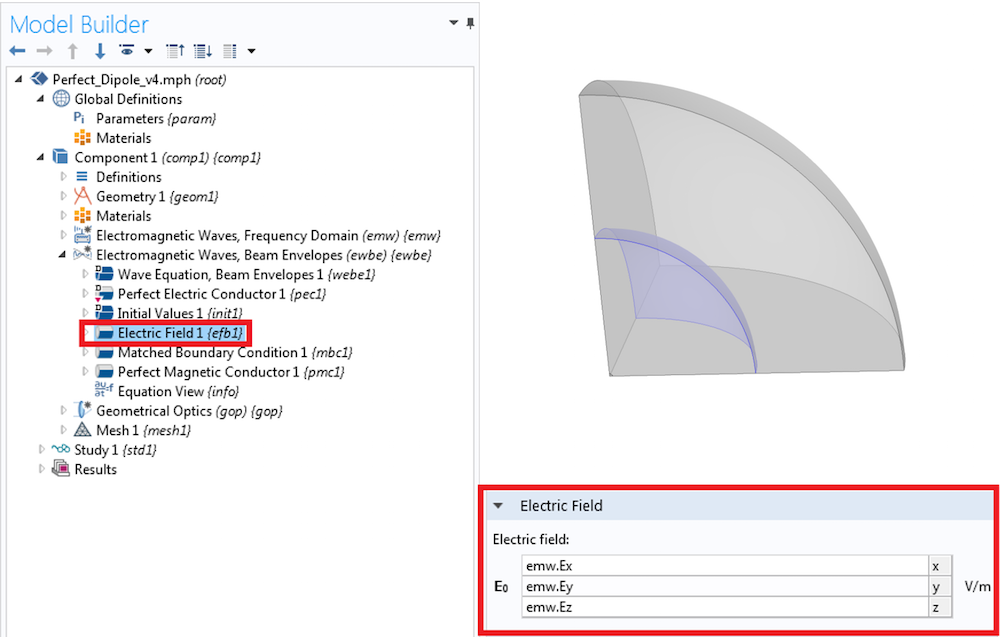
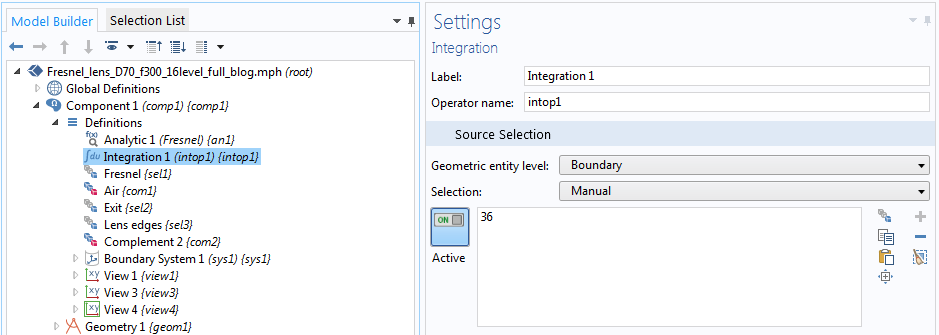
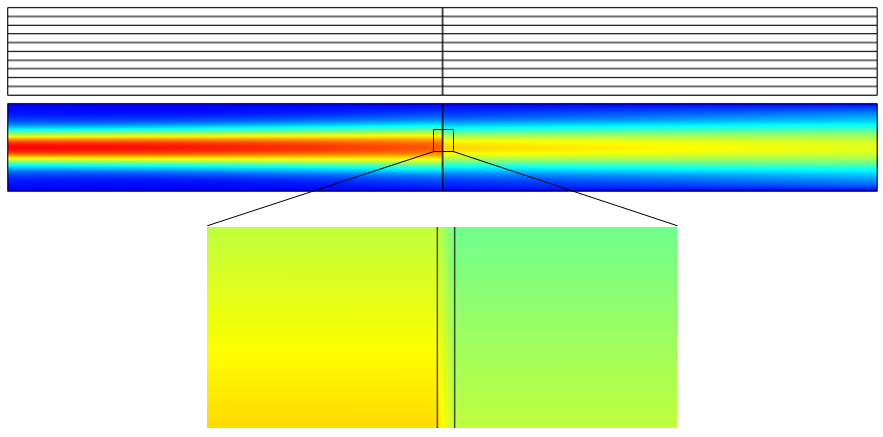
In COMSOL Multiphysics, the paraxial Gaussian beam formula is included as a built-in background field in the Electromagnetic Waves, Frequency Domain interface in the RF and Wave Optics modules. The interface features a formulation option for solving electromagnetic scattering problems, which are the Full field and the Scattered field formulations.

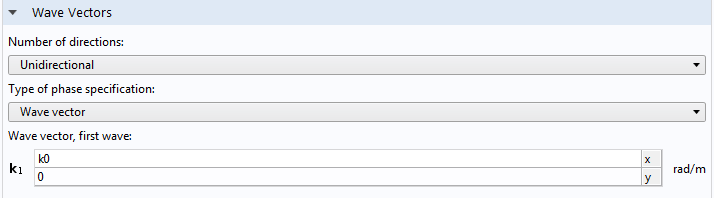
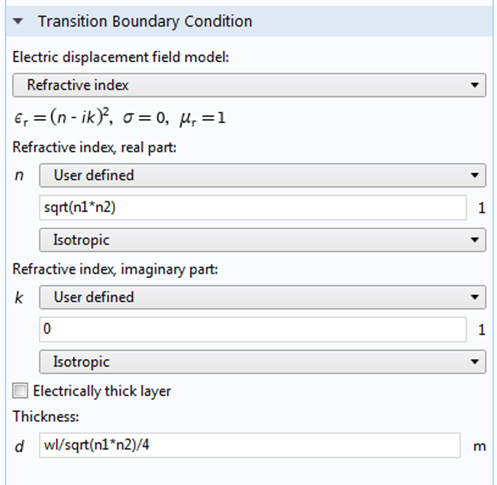
The paraxial Gaussian beam option will be available if the scattered field formulation is chosen, as illustrated in the screenshot below. By using this feature, you can use the paraxial Gaussian beam formula in COMSOL Multiphysics without having to type out the relatively complicated formula. Instead, you simply need to specify the waist radius, focus position, polarization, and the wave number.

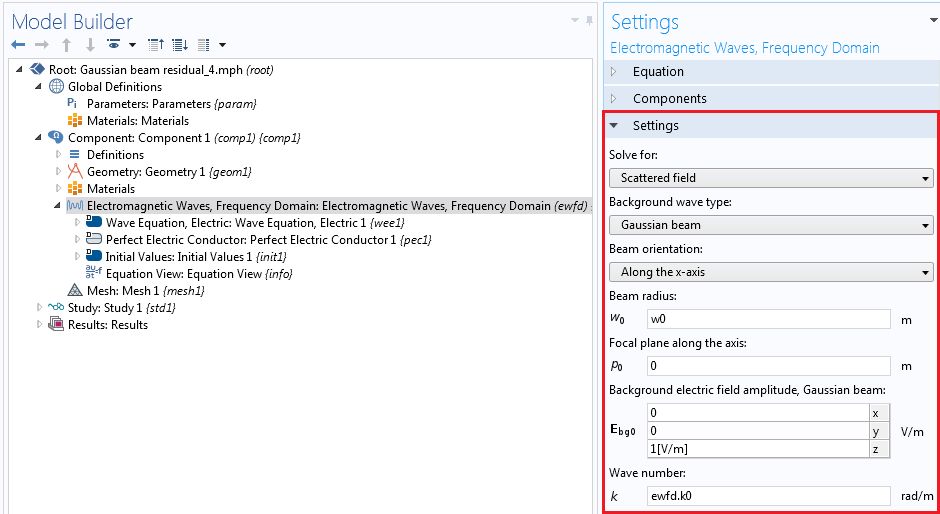
Screenshot of the settings for the Gaussian beam background field.

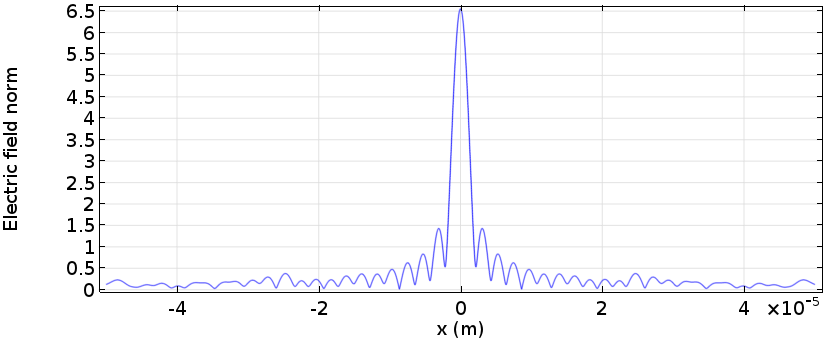
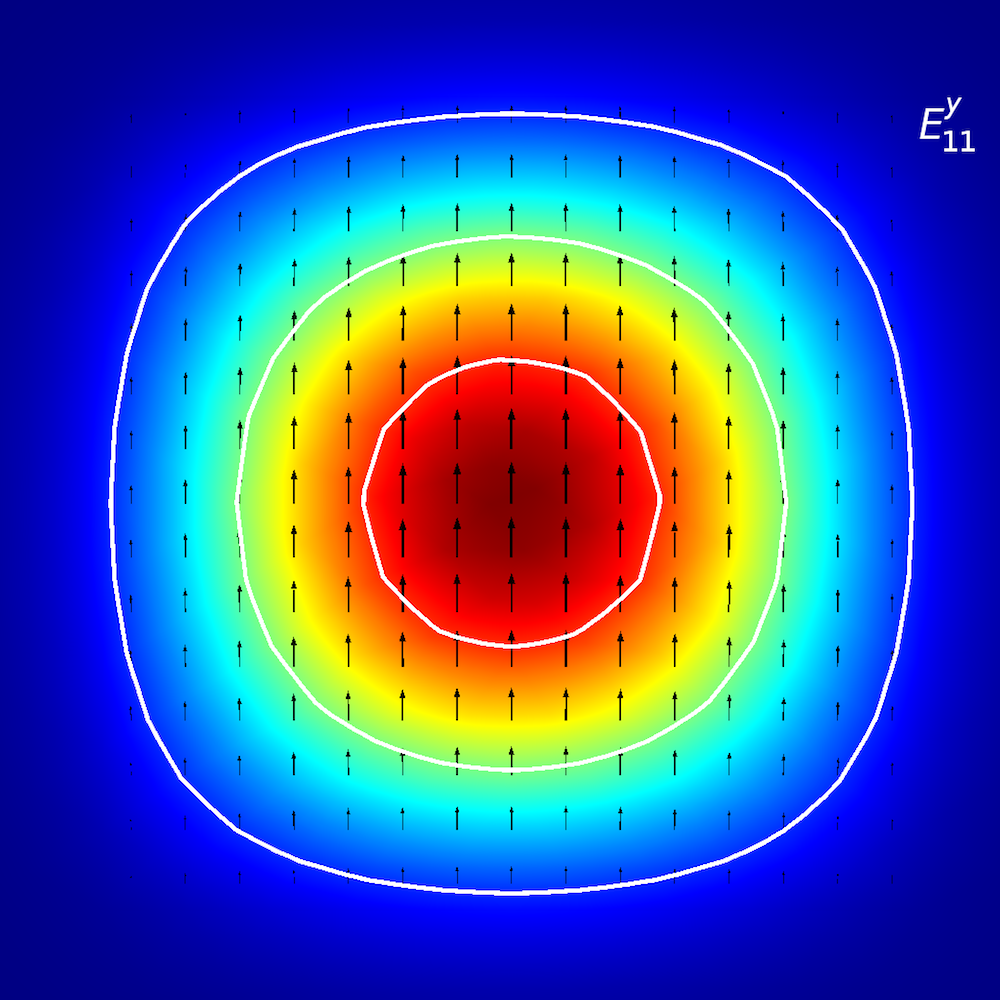
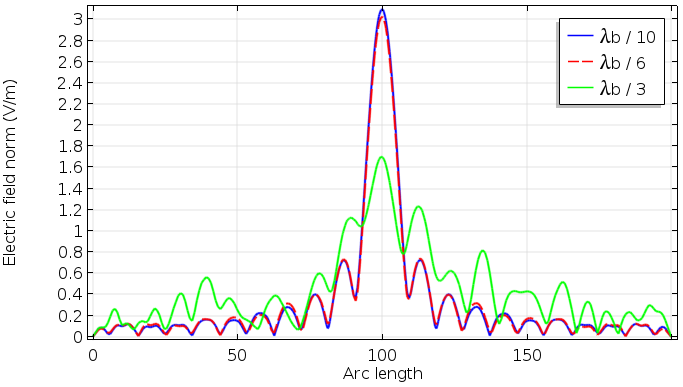
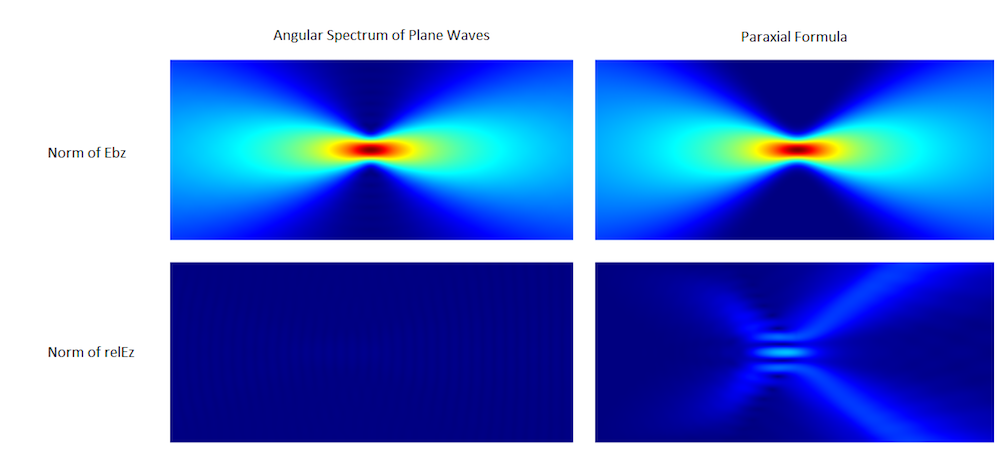
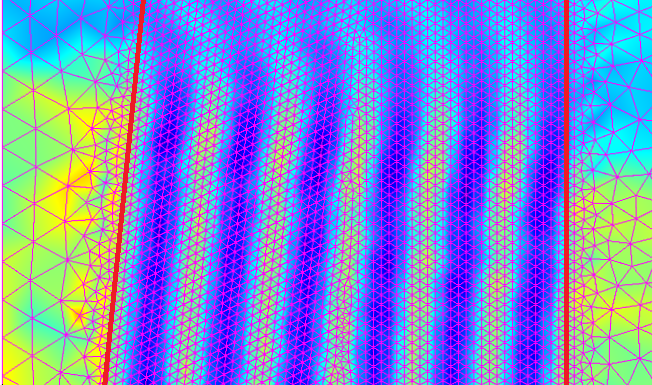
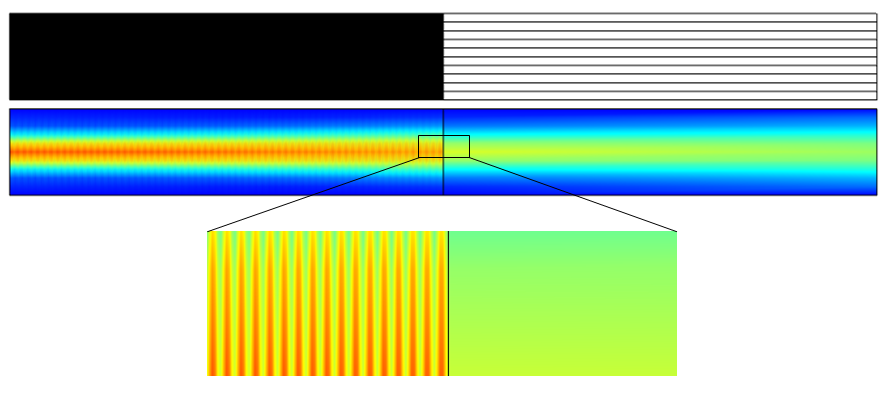
Plots showing the electric field norm of paraxial Gaussian beams with different waist radii. Note that the variable name for the background field is ewfd.Ebz.

Looking into the Limitation of the Paraxial Gaussian Beam Formula

In the scattered field formulation, the total field is linearly decomposed into the background field and the scattered field as . Since the total field must satisfy the Helmholtz equation, it follows that , where is the Laplace operator. This is the full field formulation, where COMSOL Multiphysics solves for the total field. On the other hand, this formulation can be rewritten in the form of an inhomogeneous Helmholtz equation as

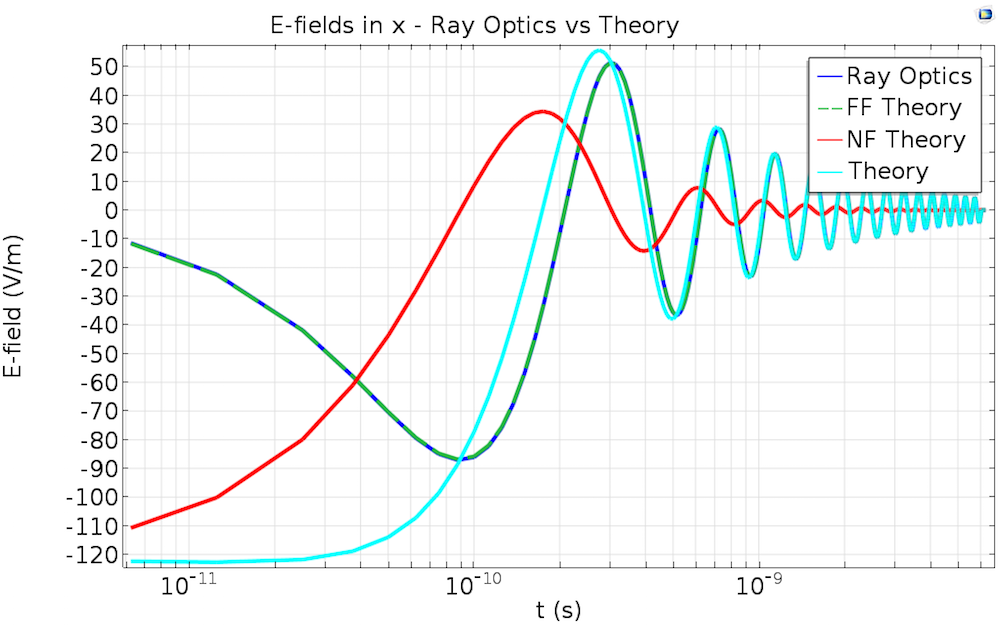
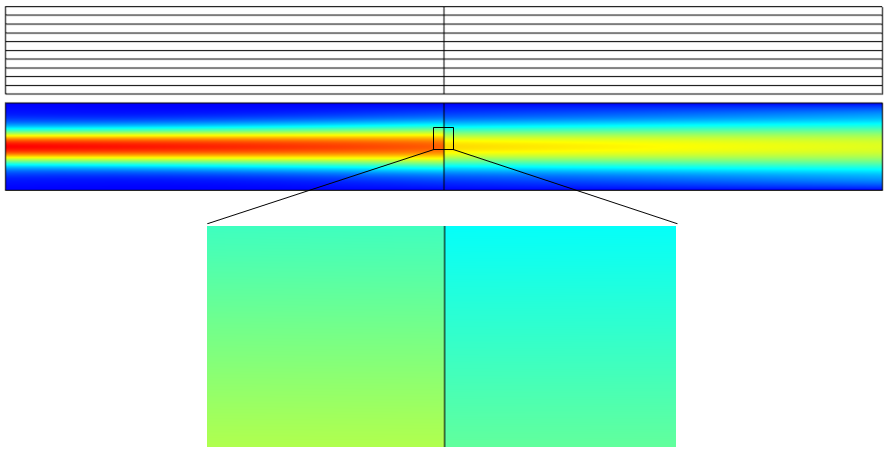
The above equation is the scattered field formulation, where COMSOL Multiphysics solves for the scattered field. This formulation can be viewed as a scattering problem with a scattering potential, which appears in the right-hand side. It is easy to understand that the scattered field will be zero if the background field satisfies the Helmholtz equation (under an approximate Sommerfeld radiation condition, such as an absorbing boundary condition) because the right-hand side is zero, aside from the numerical errors. If the background field doesn’t satisfy the Helmholtz equation, the right-hand side may leave some nonzero value, in which case the scattered field may be nonzero. This field can be regarded as an error of the background field. In other words, under certain conditions, you can qualify and quantify exactly how and by how much your background field satisfies the Helmholtz equation. Let’s now take a look at the scattered field for the example shown in the previous simulations.

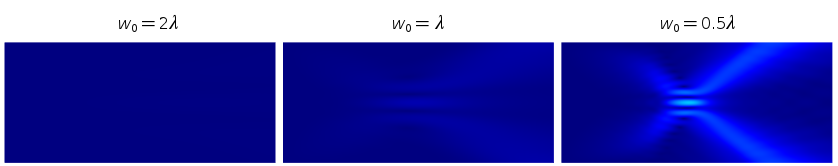
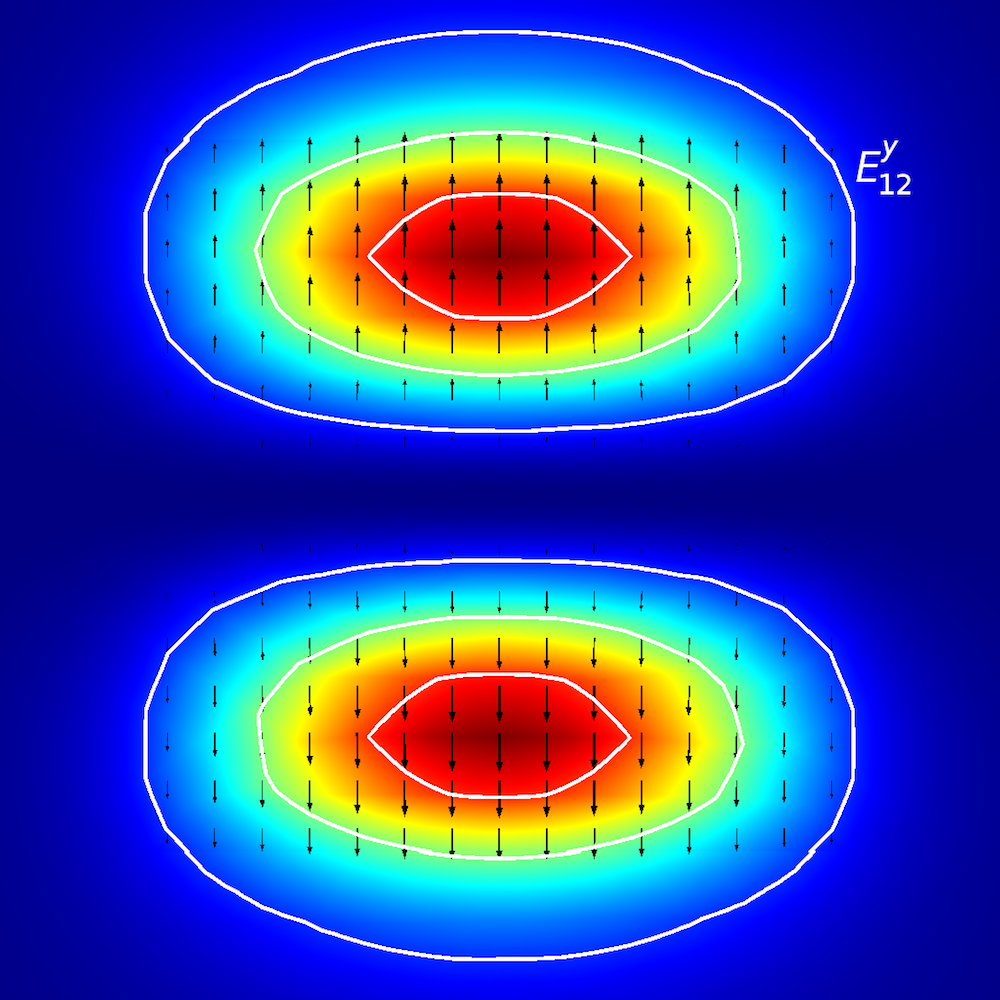
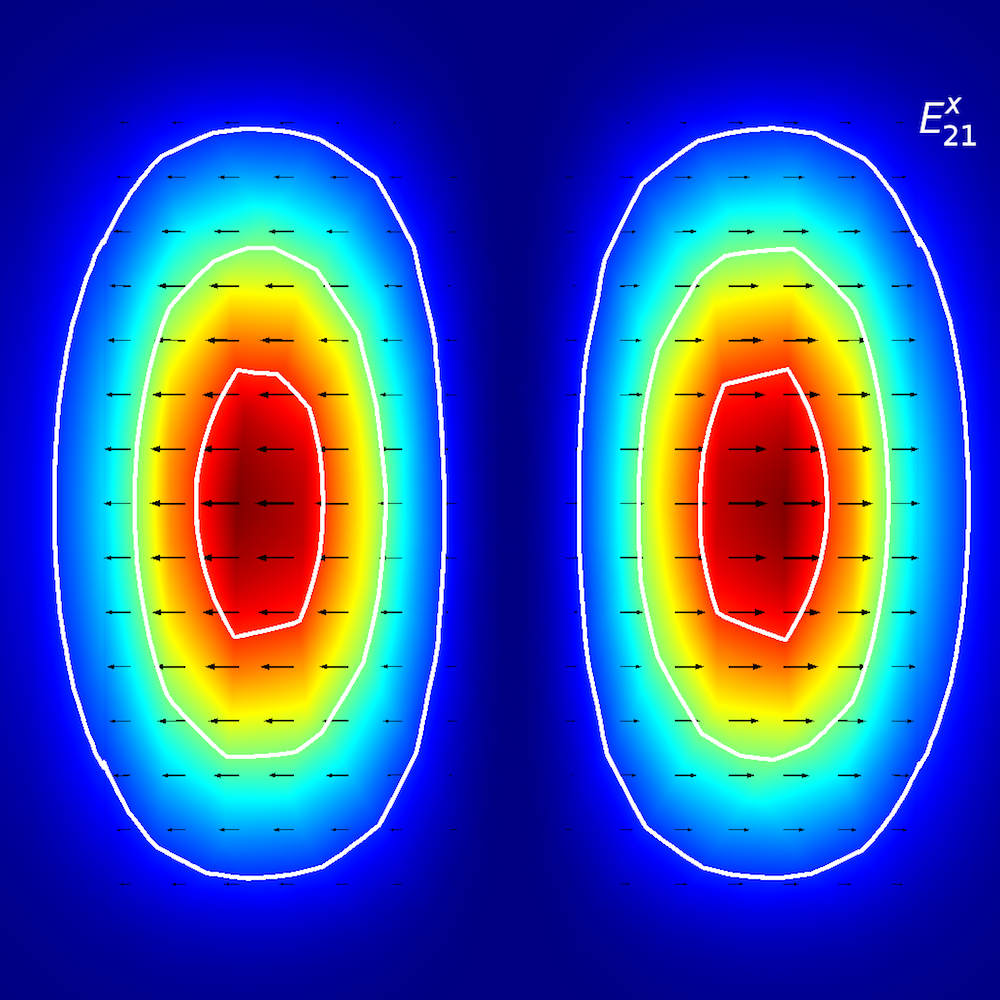
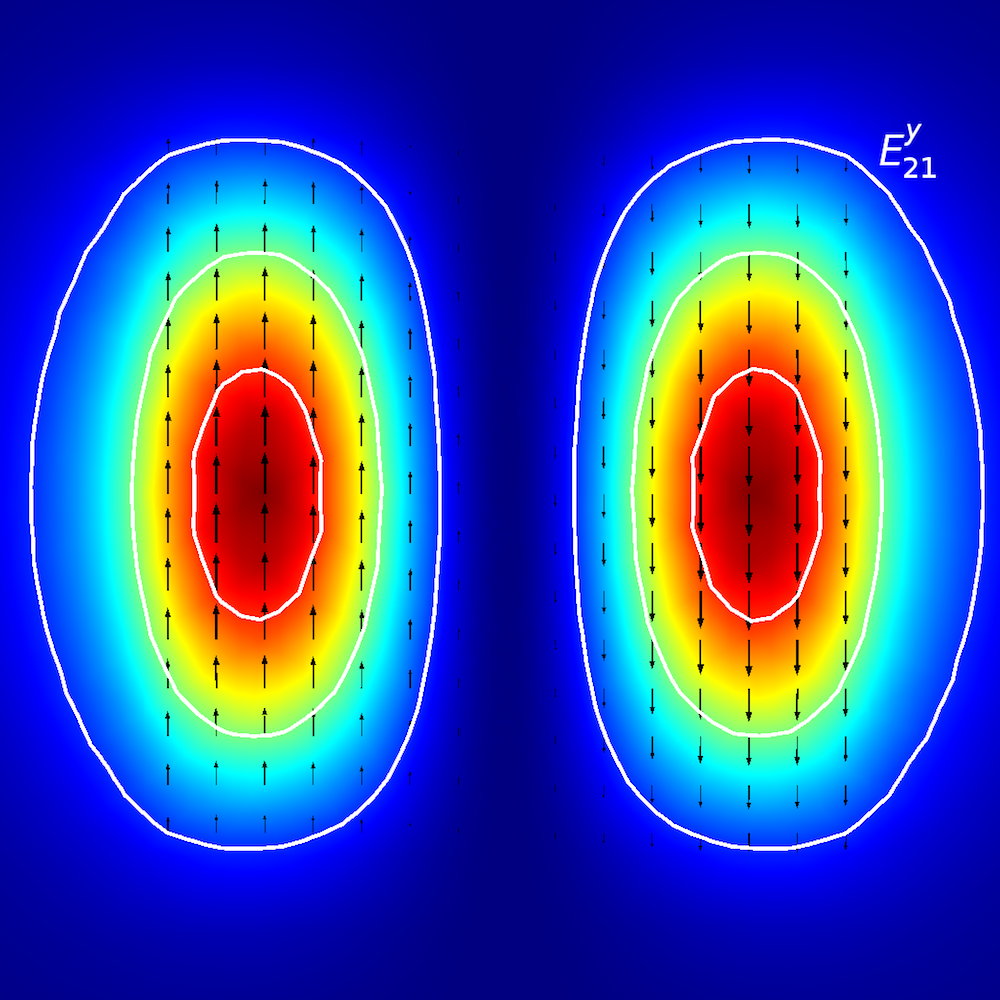
Plots showing the electric field norm of the scattered field. Note that the variable name for the scattered field is ewfd.relEz. Also note that the numerical error is contained in this error field as well as the formula’s error.

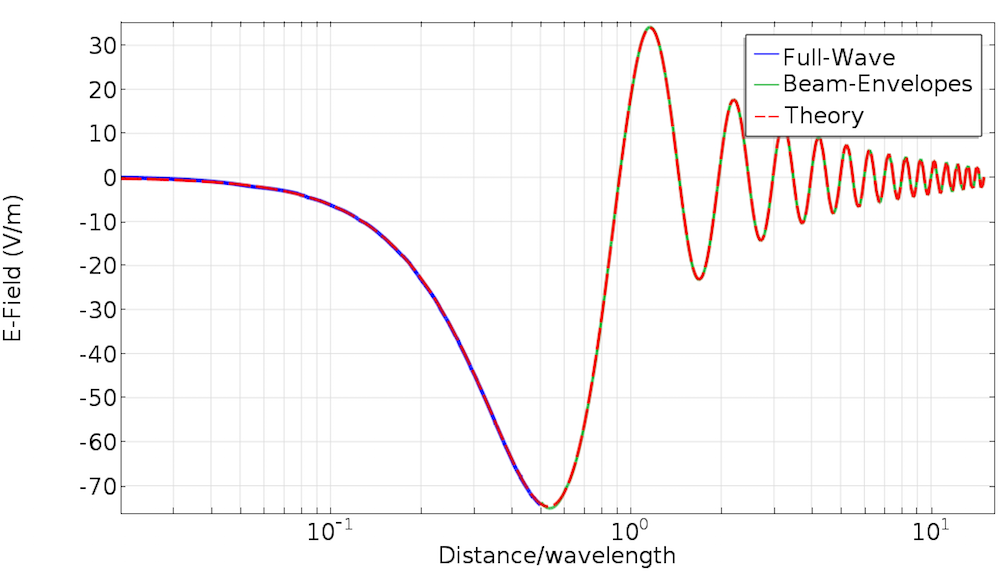
The results shown above clearly indicate that the paraxial Gaussian beam formula starts failing to be consistent with the Helmholtz equation as it’s focused more tightly. Quantitatively, the plot below may illustrate the trend more clearly. Here, the relative L2 error is defined by , where stands for the computational domain, which is compared to the mesh size. As this plot suggests, we can’t expect that the paraxial Gaussian beam formula for spot sizes near or smaller than the wavelength is representative of what really happens in experiments or the behavior of real electromagnetic Gaussian beams. In the settings of the paraxial Gaussian beam formula in COMSOL Multiphysics, the default waist radius is ten times the wavelength, which is safe enough to be consistent with the Helmholtz equation. It is, however, not a “cut-off” number, as the approximation assumption is continuous. It’s up to you to decide when you need to be cautious in your use of this approximate formula.

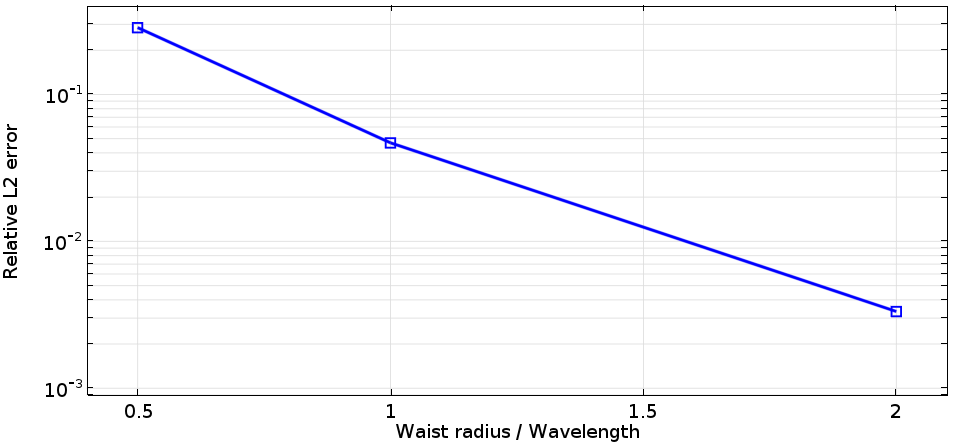
Semi-log plot comparing the relative L2 error of the scattered field with the waist size in the units of wavelength.

Checking the Validity of the Paraxial Approximation

In the above plot, we saw the relationship between the waist size and the accuracy of the paraxial approximation. Now we can check the assumptions that were discussed earlier. One of the assumptions to derive the paraxial Helmholtz equation is that the envelope function varies relatively slowly in the propagation axis, i.e., . Let’s check this condition on the x-axis. To that end, we can calculate a quantity representing the paraxiality. As the paraxial Helmholtz equation is a complex equation, let’s take a look at the real part of this quantity, .

The following plot is the result of the calculation as a function of x normalized by the wavelength. (You can type it in the plot settings by using the derivative operand like d(d(A,x),x) and d(A,x), and so on.) We can see that the paraxiality condition breaks down as the waist size gets close to the wavelength. This plot indicates that the beam envelope is no longer a slowly varying one around the focus as the beam becomes fast. A different approach for seeing the same trend is shown in our Suggested Reading section.

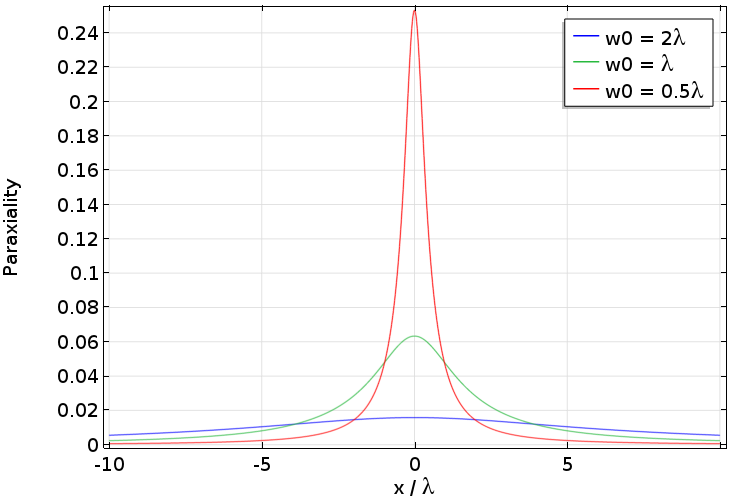
Real part of the paraxiality along the x-axis for paraxial Gaussian beams with different waist sizes.

Concluding Remarks on the Paraxial Gaussian Beam Formula

Today’s blog post has covered the fundamentals related to the paraxial Gaussian beam formula. Understanding how to effectively utilize this useful formulation requires knowledge of its limitation as well as how to determine its accuracy, both of which are elements that we have highlighted here.

There are additional approaches available for simulating the Gaussian beam in a more rigorous manner, allowing you to push through the limit of the smallest spot size. We will discuss this topic in a future blog post. Stay tuned!

Suggested Reading

• P. Vaveliuk, “Limits of the paraxial approximation in laser beams”, Optics Letters, Vol. 32, No. 8 (2007)
• Browse related topics here on the COMSOL Blog:
  • Simulating Holographic Data Storage in COMSOL Multiphysics
  • How to Simulate a Holographic Page Data Storage System

This post begins a comprehensive blog series where we will look at several approaches to multiscale modeling in high-frequency electromagnetics. Today, we will introduce the supporting theory and definitions that we will need. In subsequent posts, you will learn how to implement multiscale modeling of high-frequency electromagnetics for different scenarios in the COMSOL Multiphysics® software. Let’s get started…

Practical Scope: Antennas and Wireless Communication

Multiscale modeling is a challenging issue in modern simulation that occurs when there are vastly different scales in the same model. For example, your cellphone is approximately 15 cm, yet it receives GPS information from satellites 20,000 km away. Handling both of these lengths in the same simulation is not always straightforward. Similar issues show up in applications such as weather simulations, chemistry, and many other areas.

While multiscale modeling can be a general topic, we will focus our attention on the practical example of antennas and wireless communication. When we wirelessly transmit data via antennas, we can break the operation down into three main stages:

1. An antenna converts a local signal into free space radiation.
2. The radiation propagates away from the antenna over relatively long distances.
3. The radiation is detected by another antenna and converted into a received signal.

Modern communications require long-distance wireless data transfer via antennas.

The two length scales that we will consider for this process are the wavelength of the radiation and the distance between the antennas. To use a specific example, FM radio has a wavelength of approximately three meters. When you listen to the radio in your car, you are often ten km or more away from the radio tower. Because many antennas, such as dipole antennas, are similar in size to a wavelength, we will not consider this to be another distinct length scale. As a result, we have one length scale for the emitting antenna, a different length scale for the signal propagation from source to destination, and then the original length scale again for the receiving antenna.

Let’s go over some of the most important equations, terms, and considerations when working with multiple scales in the same high-frequency electromagnetics model.

The Friis Transmission Equation

The Friis transmission equation calculates the received power for line-of-sight communication between two antennas separated by a lossless medium. The equation is

where the subscripts r and t discriminate between the transmission antenna and the receiving antenna, G is the antenna gain, P is the power, is the reflection coefficient for impedance mismatch between antenna and transmission line, p is the polarization mismatch factor, λ is the wavelength, r is the distance between the antennas and is associated with the so-called free-space path loss, and and are the angular spherical coordinates for the two antennas.

Note that we have explicitly included two impedance mismatch terms, and so:

• P_t refers to the power provided to a transmission line attached to an emitting antenna
• P_r refers to the power received from a transmission line attached to a receiving antenna

The Friis transmission equation is derived in many texts, so we will not do so again here.

A visualization of the gain for a transmitting and receiving antenna. When using the Friis transmission equation, we require the orientation of each antenna for correct gain specification. The distance between the antennas is r.

Spherical Coordinates

Let’s now discuss spherical coordinates , since they are incredibly useful for antenna radiation and we will use them repeatedly. Starting from the Cartesian coordinates (x, y, z), we can easily express these as follows.

For convenience, we have used the actual COMSOL Multiphysics commands — sqrt(), acos(), and atan2(,) — instead of their mathematical symbols. In our simulation setup, we will also make use of the Cartesian components of the spherical unit vector .

Similar assignments can be made for the Cartesian components of and , but is the most important for our purposes. This will be discussed later in this blog series when we cover ray optics.

A given point shown in both Cartesian (x, y, z) and spherical coordinates. The unit vectors for the spherical coordinates are also included. Note that the spherical unit vectors are functions of location.

The Poynting Vector and Radiation Intensity

We are generally interested in the radiated power from antennas. The power flux in W/m² is represented by the complex Poynting vector .

Many antenna texts also use radiation intensity, which is defined as the power radiated per solid angle and measured in W/steradian. Mathematically speaking, this is . For clarity, we have included two conventions here, as it is common to use in electrical engineering, while physicists will generally be more familiar with . We can then calculate the radiated power by integrating this quantity over all angles.

Gain and Directivity

Gain and directivity are similar in that they both quantify the radiated power in a given direction. The difference is that gain relates this radiated power to the input power, whereas directivity relates this to the overall radiated power. Put more simply, gain accounts for dielectric and conductive losses and directivity does not. Mathematically, this reads as and for gain and directivity, respectively. P_in is the power accepted by the antenna and P_rad is the total radiated power. While both quantities can be of interest, gain tends to be the more practical of these two as it accounts for material loss in the antenna. Because of its prevalence and usefulness, we also include the definition of gain (in a given direction) from “IEEE Standard Definitions of Terms for Antennas”, which is: “The ratio of the radiation intensity, in a given direction, to the radiation intensity that would be obtained if the power accepted by the antenna were radiated isotropically.”

IEEE also includes three notes about gain in their definition:

1. “Gain does not include losses arising from impedance and polarization mismatches.”
2. “The radiation intensity corresponding to the isotropically radiated power is equal to the power accepted by the antenna divided by 4π.”
3. “If an antenna is without dissipative loss, then in any given direction, its gain is equal to its directivity.”

Gain, Realized Gain, and Impedance Mismatch

In practice, an actual antenna will be connected to a transmission line. Because the antenna and the transmission line may not have the same impedance, there can be a loss factor due to impedance mismatch. The realized gain is simply the gain when accounting for impedance mismatch. Mathematically, this is , where is the reflection coefficient from transmission line theory, Z_c is the characteristic impedance of the transmission line, and Z is the impedance of the antenna.

When using a lumped port with a characteristic impedance in COMSOL Multiphysics, the far-field gain that is calculated corresponds to the IEEE realized gain. This is important to mention explicitly, since various definitions of gain have changed over the last few decades. Starting with COMSOL Multiphysics version 5.3, which will be released in 2017, the variable names in the COMSOL software will be changed to match the IEEE definitions.

The realized gain and electric field from a Vivaldi antenna, simulated using COMSOL Multiphysics and the RF Module. You can find the Vivaldi Antenna tutorial model in the Application Gallery.

Receiving Antennas, Lorentz Reciprocity, and Received Power

The terms we have discussed so far have referred to antennas emitting radiation, but they are also generally applicable to receiving antennas. The reason we have put more emphasis on emission thus far is because antennas generally obey reciprocity (the Lorentz reciprocity theorem is a fixture in most antenna textbooks). Reciprocity means that an antenna’s gain in a specific direction is the same regardless of whether it is emitting in that direction or receiving a signal from that direction. Practically speaking, you can calculate the gain in any direction from a single simulation of an emitting antenna, which is easier than simulating the inverse process for each desired direction.

When we talk about receiving antennas, we are often interested in calculating the received power for an incoming signal. This can be done by multiplying the effective area, , of the antenna by the incident power flux and accounting for impedance mismatch in the line, yielding . As you may expect, this bears a striking similarity to several terms of the Friis transmission equation.

Emitter Example: A Perfect Electric Dipole

Today, we will talk about one type of emitter: the perfect electric point dipole. Depending on the literature, you may have seen this referred to as a perfect, ideal, or infinitesimal dipole. This emitter is a common representation of radiation for electrically small antennas. The solution for the field is

where is the dipole moment of the radiation source (not to be confused with the polarization mismatch) and k is the wave vector for the medium.

One breakdown of the various regions for the electromagnetic field generated from an electrically small antenna.

In this equation, there are three factors of 1/rⁿ. The 1/r² and 1/r³ terms will be more significant near the source, while the 1/r term will dominate at large distances. While the electromagnetic field will be continuous, it is common to refer to different regions of the field based on the distance from the source. One such distribution for an electrically small antenna is shown above, although there are other conventions that refer to the magnitude of kr.

Later, we will see how to calculate the fields at any distance from a given source, but the most important region for antenna communications is the far field or radiation zone, which is the region farthest away from the source. In this region, the fields take the form of spherical waves, , a fact that we will take advantage of.

We will now split up the E-field equation above into two terms. For simplicity, we will call the 1/r term the far field (FF) and the 1/r² and 1/r³ terms the near field (NF).

As mentioned before, we can calculate the radiated power in watts by integrating over all angles. Note that only the far-field term will contribute to this integral, which is a primary reason why the far field is of practical interest to antenna engineers. The total power radiated from a point dipole is , where Z₀ is the impedance of free space and c is the speed of light. The maximum gain is 1.5 and is isotropic in the plane normal to the dipole moment (e.g., the xy-plane for a dipole in ).

A note on units: The equations above are given with the traditional definition of the dipole moment in Coulomb*meters (Cm). In antenna and engineering texts, it is common to specify an infinitesimal current dipole in Ampere*meters (Am). COMSOL Multiphysics follows the engineering convention. The two definitions are related by a time derivative, so for a COMSOL software implementation, the dipole moment should be multiplied by a factor of to obtain the infinitesimal current dipole.

Receiver Example: A Half-Wavelength Dipole

We will use a perfectly conducting half-wavelength dipole as our receiving antenna.

A visual representation of radiation incident on a half-wavelength dipole antenna.

Many texts cover an infinitely thin wire, which has an impedance of and a directivity of . It is worth mentioning that the antenna impedance will change from these values for an antenna of finite radius. The receiving antenna we use here has a length of 0.47 λ and a length-to-diameter ratio of 100. With these values, we simulate an impedance of , which is close to the infinitely thin value and also agrees reasonably well with experimental values. Regrettably, there is no theoretical value to compare to this number, but this highlights the need for numerical simulation in antenna design.

The comparison between the directivity of the infinitely thin dipole and our simulated dipole antenna is shown below. Because the antenna is lossless, this is equivalent to the antenna gain. You can download the dipole antenna model here.

A comparison of the directivity for two half-wavelength antennas (oriented in z) as a function of theta. The COMSOL Multiphysics® simulation is of a finite radius cylinder and the theory is for an infinitely thin antenna.

Computing the Received Power

We can now use the Friis transmission equation to calculate the power that is emitted from a perfect point dipole and received by a half-wave dipole antenna. To use this equation, we simply need to know the gain and impedance mismatch (or realized gain), wavelength, distance between the antennas, and input power. Since we are using a point electric dipole, we have a dipole moment instead of input power and impedance mismatch. We can account for this by removing the impedance mismatch term and replacing the input power by the radiated power of the perfect electric dipole from above — effectively saying that power in equals power out.

If we assume that our emitter and detector are both located in the xy-plane, are polarization matched, and are separated by 1000 λ, as well as that the dipole moment of the emitter is 1 Am in , the Friis equation yields a received power of 380 μW. We will simulate this value in part 3 of this series for verification of our simulation technique. We can then use our simulation to confidently extract results and introduce complexity that the Friis equation cannot account for.

Concluding Thoughts

In this blog post, we have introduced the idea of multiscale modeling and discussed all of the relevant terms, definitions, and theory that we will need moving forward. For those of you with a strong background in electromagnetics and antenna design, this has likely been a quick review. If the concepts presented here are new to you, we strongly recommend further reading in a book on classical electromagnetics or antenna theory.

In the following blog posts, we will focus primarily on practical implementation of multiscale modeling in COMSOL Multiphysics and we will repeatedly refer to concepts discussed today.

Coming Up Next…

Stay tuned for more installments in our multiscale modeling blog series:

• In part 2, we will simulate the emission from a point electric dipole using the Electromagnetic Waves, Frequency Domain interface. We will discuss the Far-Field Domain node, which calculates the far-field radiation from a source, and show how the Electromagnetic Waves, Frequency Domain interface can be coupled to the Electromagnetic Waves, Beam Envelopes interface to simulate fields in the intermediate zone.
• In part 3, we will simulate a point dipole radiating to a half-wavelength dipole antenna an arbitrary distance away. For verification, we will calculate the power received by the half-wavelength dipole antenna and verify our results using the Friis transmission equation.
• In part 4, we will couple our emitting source, the point electric dipole, to a ray optics simulation using the Geometrical Optics interface.
• In part 5, we will couple the two antennas using the Geometrical Optics interface. We will again verify our results and discuss how this more general method can account for inhomogeneous media and multipath transmission.

In Part 2 of our blog series on multiscale modeling in high-frequency electromagnetics, we discuss a practical implementation of multiscale techniques in the COMSOL Multiphysics® software. We will simulate radiated fields using two different techniques and verify our results with theory. While these methods can be generally applied, we will always revolve around the practical issue of antenna-to-antenna communication. For a review of the theory and terms, you can refer to the first post in the series.

Simulating a Radiating Antenna

Let’s begin by discussing a traditional antenna simulation using COMSOL Multiphysics and the RF Module. When we simulate a radiating antenna, we have a local source and are interested in the subsequent electromagnetic fields, both nearby and outgoing from the antenna. This is fundamentally what an antenna does. It converts local information (e.g., voltage or current) into propagating information (e.g., outgoing radiation). A receiving antenna inverts this operation and changes incident radiation into local information. Many devices, such as a cellphone, act as both receiving and emitting antennas, which is what enables you to make a phone call or browse the web.

Antennas of the Atacama Large Millimeter Array (ALMA) in Chile. ALMA detects signals from space to help scientists study the formation of stars, planets, and galaxies. Needless to say, the distance these signals travel is much greater than the size of an antenna. Image licensed under CC BY 4.0, via ESO/C. Malin.

In order to keep the required computational resources reasonable, we model only a small region of space around the antenna. We then truncate this small simulation domain with an absorbing boundary, such as a perfectly matched layer (PML), which absorbs the outgoing radiation. Since this will solve for the complex electric field everywhere in our simulation domain, we will refer to this as a Full-Wave simulation.

We then extract information about the antenna’s emission pattern using a Far-Field Domain node, which performs a near-to-far-field transformation. This approach gives us information about the electromagnetic field in two regions: the fields in the immediate vicinity of the antenna, which are computed directly, and the fields far away, which are calculated using the Far-Field Domain node. This is demonstrated in a number of RF models in the Application Gallery, such as the Dipole Antenna tutorial model, so we will not comment further on the practical implementation here.

Using the Far-Field Domain Node

One question that occasionally comes up in technical support is: “How do I use the Far-Field Domain node to calculate the radiated field at a specific location?” This is an excellent question. As stated in the RF Module User’s Guide, the Far-Field Domain node calculates the scattering amplitude, and so determining the complex field at a specific location requires a modification for distance and phase. The expression for the x-component of the electric field in the far field is:

and similar expressions apply to the y- and z-component, where r is the radial distance in spherical coordinates, k is the wave vector for the medium, and emw.Efarx is the scattering amplitude. It is worth pointing out that emw.Efarx is the scattering amplitude in a particular direction, and so it depends on angular position , but not radial position. The decrease in field strength is solely governed by the 1/r term. There are also variables emw.Efarphi and emw.Efartheta, which are for the scattering amplitude in spherical coordinates.

To verify this result, we simulate a perfect electric dipole and compare the simulation results with the analytical solution, which we covered in the previous blog post. As we stated in that post, we split the full results into two terms, which we call the near- and far-field terms. We briefly restate those results here.

where is the dipole moment of the radiation source and is the unit vector in spherical coordinates.

Below, we can see the electric fields vs. distance calculated using the Far-Field Domain node for a dipole at the origin with . For comparison, we have included the Far-Field Domain node, the full theory, as well as the near- and far-field terms individually. The fields are evaluated along an arbitrary cut line. As you can see, there is overlap between the Far-Field Domain node and the far-field theory plots, and they agree with the full theory as the distance from the antenna increases. This is because the Far-Field Domain node will only account for radiation that goes like 1/r, and so the agreement improves with increasing distance as the contribution of the 1/r² and 1/r³ terms go to zero. In other words, the Far-Field Domain node is correct in the far field, which you probably would have guessed from the name.

A comparison of the Far-Field Domain node vs. theory for a point dipole source.

Using the Electromagnetic Waves, Beam Envelopes Interface

For most simulations, the near-field and far-field information is sufficient and no further work is necessary. In some cases, however, we also want to know the fields in the intermediate region, also known as the induction or transition zone. One option is to simply increase the simulation size until you explicitly calculate this information as part of the simulation. The drawback of this technique is that the increased simulation size requires more computational resources. We recommend a maximum mesh element size of for 3D electromagnetic simulations. As the simulation size increases, the number of mesh elements increases, and so do the computational requirements.

Another option is to use the Electromagnetic Waves, Beam Envelopes interface, which here we will simply refer to as Beam-Envelopes. As discussed in a previous blog post, Beam-Envelopes is an excellent choice when the simulation solution will have either one or two directions of propagation, and will allow us to use a much coarser mesh. Since the phase of the emission from an antenna will look like an outgoing spherical wave, this is a perfect solution for determining these fields. We perform a Full-Wave simulation of the fields near the source, as before, and then use Beam-Envelopes to simulate the fields out to an arbitrary distance, as required.

The simulation domain assignments. If the outer region is assigned to PML, then a Full-Wave simulation is performed everywhere. It is also possible to solve the inner region using a Full-Wave simulation and the outer region using Beam-Envelopes, as we will discuss below. Note that this image is not to scale, and we have only modeled 1/8 of the spherical domain due to symmetry.

How do we couple the Beam-Envelopes simulation to our Full-Wave simulation of the dipole? This can be done in two steps involving the boundary conditions at the interface between the Full-Wave and Beam-Envelopes domains. First, we set the exterior boundary of the Full-Wave simulation to PMC, which is the natural boundary condition for that simulation. The second step is to set that same boundary to an Electric Field boundary condition for Beam-Envelopes. We then specify the field values in the Beam-Envelopes Electric Field boundary condition according to the fields computed from the Full-Wave simulation, as shown here.

The Electric Field boundary condition in Beam-Envelopes. Note that the image in the top right is not to scale.

A Matched Boundary Condition is applied to the exterior boundary of the Beam-Envelopes domain to absorb the outgoing spherical wave. The remaining boundaries are set to PEC and PMC according to symmetry. We must also set the solver to Fully Coupled, which is described in more detail in two blog posts on solving multiphysics models and improving convergence from a previous blog series on solvers.

If we again examine the comparison between simulation and theory, we see excellent agreement over the entire simulation range. This shows that the PMC and Electric Field boundary conditions have enforced continuity between the two interfaces and they have fully reproduced the analytical solution. You can download the model file in the Application Gallery.

A comparison of the electric field of the Full-Wave and Beam-Envelopes simulations vs. the full theory.

Concluding Thoughts on Simulating a Radiating Source in COMSOL Multiphysics®

In today’s blog post, we examined two ways of computing the electric field at points far away from the source antenna and verified the results using the analytical solution for an electric point dipole. These two techniques are using the Far-Field Domain node from a Full-Wave simulation and linking a Full-Wave simulation to a Beam-Envelopes simulation. In both cases, the fields near the source and in the far field are correctly computed. The coupled approach using Beam-Envelopes has the additional advantage in that it also computes fields in the intermediate region. In the next post in the series, we will combine the calculated far-field radiation with a simulation of a receiving antenna and determine the received power. Stay tuned!

Read the Full Series

• Browse the other posts in the Multiscale Modeling for High-Frequency Electromagnetics blog series

In Part 3 of our series on multiscale modeling in high-frequency electromagnetics, let’s turn our attention to the receiving antenna. We’ve already covered theory and definitions in Part 1 and radiating antennas in Part 2. Today, we will couple a radiating antenna at one location with a receiving antenna 1000 λ away. For verification, we will calculate the received power via line-of-sight transmission and compare it with the Friis transmission line equation that we covered in Part 1.

Simulating the Background Field

In the simulation of our receiving antenna, we will use the Scattered Field formulation. This formulation is extremely useful when you have an object in the presence of a known field, such as in radar cross section (RCS) simulations. Since there are a number of scattered field simulations in the Application Gallery, and it has been discussed in a previous blog post, we will assume a familiarity with this technique and encourage you to review those resources if the Scattered Field formulation is new to you.

The Scattered Field formulation is useful for computing a radar cross section.

When comparing the implementation we will use here with the scattering examples in the Application Gallery, there are two differences that need to be referenced explicitly. The first is that, unlike the scattering examples, we will use a receiving antenna with a Lumped Port. With the Lumped Port excitation set to Off, it will receive power from the background field. This is automatically calculated in a predefined variable, and since the power is going into the lumped power, the value will be negative. The second difference, which we will spend more time discussing, is that the receiving antenna will be in a separate component than the emitting antenna and we will have to reference the results of one component in the other to link them.

Multiple Components in the Same Model

What does it mean when we have two or more components in a model? The defining feature of a component is that it has its own geometry and spatial dimension. If you would like to have a 2D axisymmetric geometry and a 3D geometry in the same simulation, then they would each require their own component. If you would like to do two 3D simulations in the same model, you only need one component, although in some situations it can be beneficial to separate them anyways.

Let’s say, for example, that you have two devices with relatively complicated geometries. If they are in the same component, then anytime you make a geometric change to one, they both need to be rebuilt (and remeshed). In separate components this would not be the case. Another common use of multiple components is submodeling, where the macroscopic structure is analyzed first and then a more detailed analysis is performed on a smaller region of the model. When we split into components, however, we then need to link the results between the simulations.

In our case, we have two antennas at a distance of 1000 λ. Separating them into distinct components is not strictly required, but we are going to do it anyways to keep things general. We will add in ray tracing later in this series and some users may find this multiple component method useful with an arbitrarily complex ray tracing geometry.

While we go through the details, it’s important that we have a clear image of the big picture. The main idea that we are pursuing in this post is that we first simulate an emitting antenna and calculate the radiated fields in a specific direction. Specifically, this is the direction of the receiving antenna. We then account for the distance between the antennas and use the calculated fields as the background field in a Scattered Field formulation for the receiving antenna. The emitting antenna is centered at the origin in component 1 and the receiving antenna is centered at the origin in component 2. Everything we will discuss here is simply the technical details of determining the emitted fields from the first simulation and using them as a background field in a second simulation.

Note: The overwhelming majority of the COMSOL Multiphysics® software models only have one component and only should have one component. Ensure that you have a sufficient need for multiple components in your model before implementing them, as there is a very real possibility of causing yourself extra work without benefit.

Connecting Components with Coupling Operators

There are a number of coupling operators, also known as component couplings, available in COMSOL Multiphysics. Generally speaking, these operators map the results from one spatial location to another. Said in another way, you can call for results in one location (the destination), but have the results evaluated at a separate location (the source). While this may seem trivial at first glance, it is an incredibly powerful and general technique. Let’s look at a few specific examples:

1. We can evaluate the maximum or minimum value of a variable in a 3D domain, but call that result globally. This is a 3D to 0D mapping and allows us to create a temperature controller. Note that this can also be used with boundaries or edges, as well as averages or spatial integrations.
2. We can extrude 2D simulation results to a 3D domain. This allows you to exploit translation symmetry in one physics (2D) and use the results in a more complex 3D model.
3. We can project 3D data onto a 2D boundary (or 2D to 1D, etc.) A simple example of this is creating shadow puppets on a wall, but can also be useful for analyzing averages over a cross section.

As mentioned above, we want to simulate the emitting antenna (just like we did in Part 2 of the series) and calculate the radiated fields at a distance of 1000 λ. We then use a component coupling to map the fields to being centered about the origin in component 2.

Mapping the Radiated Fields

If we look at the far-field evaluation discussed in Part 2, we know that the x-component of the far field at a specific location is

The only complication is determining where to calculate the scattering amplitude. This is because component couplings need the source and destination to be locations that exist in the geometry. We don’t want to define a sphere in component 1 at the actual location of the receiving antenna, since that defeats the entire purpose of splitting the two antennas into two components. What we will do instead is create a variable for the magnitude of r, and then evaluate the scattering amplitude at a point in the geometry that shares the same angular coordinates, , as the point we are actually interested in. In the image below, we show the point where we would like to evaluate the scattering amplitude.

Image showing where the scattering amplitude should be calculated and how the coordinates of that point can be determined.

Defining the Point and Coupling Operator

We add a point to the geometry using the rescaling of the Cartesian coordinates shown in the above figure. Only x is shown in the figure, but the same scaling is also applied to y and z. For the COMSOL Multiphysics implementation, shown below, we have assumed that the receiving antenna is centered at a location of (1000 λ, 0, 0), and the two parameters used are ant_dist = and sim_r = .

The required point for the correct scattering amplitude evaluation.

Note that we create a selection group from this point. This is so that it can be referenced without ambiguity. We then use this selection for an integration operator. Since we are integrating only over a single point, we simply return the value of the integrand at that point similar to using a Dirac delta function.

The integration operator is defined using the selection group for the evaluation point.

Running the Background Field Simulation in COMSOL Multiphysics®

The above discussion was all about how to evaluate the scattering amplitude at the correct location. The only remaining step is to use this in a background field simulation of the half-wavelength dipole discussed in Part 1. When we add in the known distance between the antennas, we get the following:

The variable definition for r. Note that this is defined in component 2.

The background field settings.

In the settings, we see that the expression used for the background field in x is comp1.intop1(emw.Efarx)*exp(-j*k*r)/(r/1[m]), which matches the equation cited above. Also note that r is defined in component 2, while intop1() is defined in component 1. Since we are calling this from within component 2, we need to include the correct scope for the coupling operator, comp1.intop1(). The remainder of the receiving antenna simulation is functionally equivalent to other Scattered Field simulations in the Application Gallery, so we will not delve into the specifics here.

It is interesting to note that running either the emission or background field simulations by themselves is quite straightforward. All of the complication in this procedure is in correctly calculating the fields from component 1 and using them in component 2. All of this heavy lifting has paid off in that we can now fully simulate the received power in an antenna-to-antenna simulation, and the agreement between the simulated power and the Friis transmission equation is excellent. We can also obtain much more information from our simulation than we can purely from the Friis equation, since we have full knowledge of the electromagnetic fields at every point in space.

It is worth mentioning one final point before we conclude. We have only evaluated the far field at an individual point, so there is no angular dependence in the field at the receiving antenna. Because we are interested in antennas that are generally far apart, this is a valid approximation, although we will discuss a more general implementation in Part 4.

Concluding Thoughts on Coupling Radiating and Receiving Antennas

We have now reached a major benchmark in this blog series. After discussing terminology in Part 1 and emission in Part 2, we can now link a radiating antenna to a receiving antenna and verify our results against a known reference. The method we have implemented here can also be more useful than the Friis equation, as we have fully solved for the electromagnetic fields and any polarization mismatch is automatically accounted for.

There is one remaining issue, however, that we have not discussed. The method used here is only applicable to line-of-sight transmission through a homogeneous medium. If we had an inhomogeneous medium between the antennas or multipath transmission, that would not be appropriately accounted for either by this technique or the Friis equation. To solve that issue, we will need to use ray tracing to link the emitting and receiving antennas. In Part 5 of this blog series, we will show you how we can link a radiating source to a ray optics simulation.

Further Reading

• Browse previous posts in the Multiscale Modeling in High-Frequency Electromagnetics blog series

Welcome back to our discussion on multiscale modeling in high-frequency electromagnetics. Multiscale modeling is a simulation challenge that arises when there are vastly different scales in a single simulation, such as the size of an antenna compared to the distance between the antenna and its target. Today, in Part 4 of the series, we will examine how we can construct a multiscale model by coupling a Full-Wave antenna simulation with a geometrical optics simulation using the Ray Optics Module.

Using the Ray Optics Module for Multiscale Modeling

In Part 2 of the blog series, we used the Electromagnetic Waves, Frequency Domain interface, which we call a Full-Wave simulation, and a Far-Field Domain node to determine the electric field in the far field. We then coupled a Full-Wave simulation to the Electromagnetic Waves, Beam Envelopes interface (or a Beam-Envelopes simulation) in order to precisely calculate fields in any region, regardless of the distance from the source.

The Far-Field Domain and Beam-Envelopes solutions that we looked at in the previous blog post are effective, but they share one noteworthy restriction. In each case, we assumed that a homogeneous domain surrounded the antenna in all directions. For many situations, this information is sufficient. In other simulations, you may not have a homogeneous domain surrounding your antenna and you need to account for issues like atmospheric refraction or reflection off of nearby buildings. These simulations require a different approach.

A model of several hotels in Las Vegas. A directional antenna emits rays toward the ARIA® Resort & Casino.

The Geometrical Optics interface in the Ray Optics Module, an add-on product to the COMSOL Multiphysics® software, regards EM waves as rays. This interface can account for spatially varying refractive indices, reflection and refraction from complicated geometries, and long propagation distances. However, these features come with a tradeoff. Since waves are treated as rays, this approach neglects diffraction. In other words, we are assuming that the wavelength of light is much smaller than any geometric features in our environment. You can read a more thorough description of ray optics in a previous blog post.

Modeling Coupled Antennas: Preparing for Ray Optics

As you may recall, we introduced an approach to coupling a radiating and receiving antenna in Part 3 of this series. When incorporating ray optics into our multiscale modeling, we are required to use a similar but more generalized approach. Before we show you how to set up a geometrical optics simulation in COMSOL Multiphysics, let’s first review this alternate method.

Mapping the Radiated Fields

As a quick refresher, we are interested in calculating the fields at the location of the receiving antenna using the following equation:

We previously used an integration operator on a single point to calculate this along the line directly between the two antennas. We now wish to retain the angular dependence, so we need to recalculate this equation for each point in the receiving antenna’s domain. Since it is impractical to add numerous points and integration operators, we need to establish a more general technique.

To do so, we replace the integration operator with a General Extrusion operator. As before, we create a variable for the magnitude of r. We then use the General Extrusion operator to evaluate the scattering amplitude at a point in the geometry that shares the same angular coordinates, , as the point in which we are actually interested.

To demonstrate this concept, we use a figure that is slightly more involved than that from the previous post. Note that the subscripts 1, 2, and r in represent a vector in component 1, a vector in component 2, and the offset between the antennas, respectively.

Image showing where the scattering amplitude should be calculated and how the coordinates of that point can be determined.

As we previously outlined, the primary complication is determining where to calculate the scattering amplitude. We want the fields at the point , which requires calculating the scattering amplitude at . The complication, of course, is that each point in the domain around the receiving antenna (each vector ) will have its own evaluation location . We evaluate this by again rescaling the Cartesian coordinates, but instead of doing it for a single point, we define it inside of the general operator so that it can be called from any location. From the above figure, we know that this point is , with corresponding equations for y and z. The operator is defined in component 1, so the source will be defined in that component. It will be called from component 2, so the x, y, z in the following expressions refer to x₂, y₂, z₂ in the above figure.

The General Extrusion operator used for the scattering amplitude calculation. Note that this is defined in component 1.

Storing the Radiated Fields in a Dummy Variable

As a bookkeeping step, we store the calculated fields in a “dummy” variable. By a dummy variable, we mean that we add in an extra dependent variable that takes the value of a calculation determined elsewhere. We do this for two reasons.

The first reason is that most variables in COMSOL Multiphysics are calculated on demand from the dependent variables. In an RF simulation, for example, the dependent variables are the three Cartesian components of the electric field: Ex, Ey, and Ez. These are determined when computing the solution. In postprocessing, every other value (electric current, magnetic field, etc.) is calculated from the electric field when required. In most cases, this is a fast and seamless process. In our case, each field evaluation point requires a general extrusion of a scattering amplitude, and each scattering amplitude point requires a surface integration as defined in the Far-Field Domain node. This can take a while and we want to ensure that we perform this calculation only once.

The second reason why we do this has to do with the element order. The Scattered Field formulation requires a background electric field. COMSOL Multiphysics then calculates the magnetic field using the differential form of Faraday’s law (also known as the Maxwell-Faraday equation). This requires taking spatial derivatives of the electric field. There are no issues when taking the spatial derivatives of an analytical function like a plane wave or Gaussian beam, but it can cause a discretization issue when applied to a solved-for variable. This is a rather advanced topic, which you can find out more about in an archived webinar on equation-based modeling.

By using a cubic dummy variable to store the electric field, we can take a spatial derivative of the electric field and still obtain a well-resolved magnetic field for use in the Scattered Field formulation. Without the increased order of the dummy variable, the magnetic field used would be underresolved. Below, you can see what it looks like to put the General Extrusion operator together with the dummy variable setup. The variable r is identical to the one used in Part 3 of this blog series and is defined in component 2.

The dummy variable implementation. Notice that the dummy variable components are called Ebx, Eby, and Ebz.

The only remaining step is to use the dummy variables — Ebx, Eby, and Ebz — in a background field simulation of the half-wavelength dipole discussed in Part 1 and Part 3.

This technique isn’t actually very good for this particular problem. There may be situations where it is useful, but the technique from Part 3 is preferred in the vast majority of cases. The received power from the two simulations is extremely close, but this method takes much longer to calculate and the file size increases drastically. In the demo examples for this post, this method took several times longer than the previous simulation method. While you may conclude that this is not a terribly useful step overall, it is useful when we incorporate ray optics into our multiscale modeling, as discussed in the next section.

Setting Up a Geometrical Optics Simulation in the COMSOL® Software

A geometrical optics simulation implicitly assumes that every ray is already in the far field. Earlier in the blog series, we saw that the Far-Field Domain feature correctly calculates the electric field at arbitrary points in the far field. Here, we use that information as the input for rays in a geometrical optics simulation. The simulation geometry, symmetry, and electric dipole point source used are the same as in Part 2.

The domain assignments for the simulation. The Full-Wave simulation is performed over the entire domain, with the outer region set as a perfectly matched layer (PML). The geometrical optics simulation is only performed in this outer region. Note that this image is not to scale.

With the domains assigned, we select the Geometrical Optics interface, change the Intensity computation to Compute intensity, and select the Compute phase check box. These steps are required to properly compute the amplitude and phase of the electric field along the ray trajectory.

Settings for the Geometrical Optics interface. The Intensity computation is set to Compute intensity and the Compute phase check box is selected.

We also apply an Inlet boundary condition to the boundary between the Full-Wave simulation domain and Geometrical Optics domain. The inlet settings can be seen in the image below, but let’s walk through them one at a time. First, the Ray Direction Vector section is configured. This will launch the rays normal to the curved surface we’ve selected for the inlet — in other words, radially outwards. The variables Etheta and Ephi are calculated from the scattering amplitude according to

with a similar assignment for Ephi.

This equation comes from our previous blog post about using the Far-Field Domain node to calculate the fields at an arbitrary location. These variables are used to specify the initial phase and polarization of the rays. The variable specifies the correct spatial intensity distribution for the rays (as antennas generally do not emit uniformly) and is calculated according to , where Z is the impedance of the medium.

The initial radius of curvature has two factors. The parameter is the radius of the spherical boundary that we are launching the rays from and will correctly initialize the curvature of the ray wavefront.

Finally, we use the Cartesian components of our spherical unit vector to specify the initial principal curvature direction. This ensures that the correct polarization orientation is imparted to the rays. The wavefront shape here must be set to Ellipsoid — even though the surface is technically a sphere — because we need to be able to specify a preferred direction for polarization. If we choose Spherical, then each orientation is degenerate and we cannot make that specification.

The settings for the Inlet boundary condition in the Geometrical Optics interface. Note that you can click the image to expand it.

Beyond setting the correct frequency, the only other setting here is the placement of a Freeze Wall condition on the exterior boundary to stop the rays. Let’s take a look at the results vs. theory. As before, we express the full solution for a point dipole as a sum of two contributions, which we have labeled near field (NF) and far field (FF).

The electric fields from a geometrical optics simulation compared against theory. Geometrical optics is always in the far field, so we see excellent agreement as the distance from the source increases. For reference, the far-field domain results from the previous post would overlap exactly with the ray optics and FF theory lines.

As mentioned before, the Geometrical Optics interface is necessarily in the far field, so we do not expect to be able to correctly capture the near-field information as we did in the Beam-Envelopes solution in Part 2. This can also be seen because we seeded the ray tracing simulation with data from the Far-Field Domain node calculation. It is therefore unsurprising that there is disagreement near the source, but we can clearly see that the results match with theory as the distance from the source increases.

Summary of Multiscale Modeling Techniques

From looking solely at the above plot, we have to ask ourselves: “What have we actually gained here?”

This is a fair question, because the plot shown above could have been constructed directly from any of the techniques covered in the series so far. To make this clear, let’s review each of them.

A summary of the multiscale modeling techniques we have covered in this blog series.

Note that any of these techniques will require a Full-Wave simulation of the radiation source. This generally requires the RF Module, although there is a subset of radiation sources that can be modeled using the Wave Optics Module instead. The Far-Field Domain node is available in both the RF and Wave Optics modules.

We originally motivated this discussion by talking about signal transmission from one antenna to another, and solved that simulation using the Far-Field Domain node in the last post. In the next blog post in this series, we’ll redo that simulation using the Geometrical Optics interface introduced here.

Access the model discussed in this blog post and any of the model examples highlighted throughout this blog series by clicking on the button above.

ARIA is a registered trademark of CityCenter Land, LLC.

While electro-optic (EO) routers are currently used in on-chip optical communication systems, they may require too much power for some applications. In these situations, we can look to monolithically integrated magneto-optic (MO) routers as low-power alternatives. Designing these routers can be challenging. With multiphysics simulation, we can analyze on-chip MO routers and the manufacturing techniques used to create them.

Taking a Closer Look at Magneto-Optic Routers

Modern optical communication systems commonly use EO routers and macroscale MO devices. Each device, however, has its own drawbacks. EO routers require an electric field and often have operation voltages in the kilovolt range, while macroscale MO devices don’t allow for scalable solutions. The quest for small, low-power optic routing alternatives is thus an important focus for specialized researchers within this field. This search is complicated, as various specializations within physics and engineering are required to address the study and interaction of magnetism, magnetic materials, and light.

Scanning electron micrograph of an unpolished silicon-on-insulator rib waveguide used for optical routers on a chip. Image credit: J. Tioh, “Interferometric switches for transparent networks: development and integration,” 2012, Graduate Theses and Dissertations. Paper 12487.

One potential solution involves integrating optical components onto a silicon substrate to create an MO routing solution on a chip. This option reduces both the size and operation power of the device and can potentially enable new technologies like light processors. But before monolithically integrated MO routers become commonplace, there are still a few hurdles that this technology needs to overcome.

Standard industry practices, for instance, present a challenge when it comes to manufacturing monolithically integrated MO routers. To introduce new technology with minimal industry disruptions, standard practices must be used. In this case, silicon should be used as a base substrate and the combining materials must be compatible with silicon for successful monolithic integration. But bonding silicon and the suitable magneto-optic materials can be quite difficult using standard industry practices due to their crystal structures. As a result, the materials tend to become brittle and crack, significantly increasing optical losses.

Multiphysics simulation offers potential solutions to such challenges. These tools can help the research community identify optimal designs and manufacturing techniques for monolithically integrated MO routers. For his doctoral dissertation at Iowa State University, John Pritchard, an engineer who works within this field, turned to the COMSOL Multiphysics® software to provide new insight into the design and future of on-chip MO routers.

Analyzing the Components of an On-Chip MO System with COMSOL Multiphysics®

When analyzing an on-chip MO system, Pritchard chose to focus on a few key design elements. One point of focus was analyzing a codirectional coupler, a device that is commonly found in interferometer designs. The power coupling coefficients of a codirectional coupler vary based on the distance between the coupling section length and coupled waveguides. Through his simulation work, Pritchard determined how to generate an ideal power coupler coefficient by choosing a specific coupler length.

3D simulation results for the codirectional coupler. Copyright © John Pritchard.

Another point of analysis was an on-chip optical waveguide. The goal here was to design a rib waveguide that minimizes energy loss and maintains a sufficient beam profile throughout the device. To achieve this, Pritchard used silicon as the rib waveguide’s transmission medium, since it is suitably transparent to infrared light and useful for integration with electronic devices. Further, a low-index cladding model was placed between the substrate and waveguide to stop the optical mode from leaking out.

The optical mode of an SOI rib waveguide. Copyright © John Pritchard.

As for the waveguide’s silicon-on-insulator (SOI) platform, Pritchard used a buried oxide insulator on a silicon substrate. This waveguide configuration enabled him to confine relatively large optical modes in the waveguide and avoid harming the single-mode operation. Subsequent simulations of the configuration revealed that the optical mode is well confined within the waveguide and that this geometry can be used to design an interferometer. Pritchard also performed a frequency analysis of the top view of the design, as seen in the animation below and to the left. This waveguide design was deemed a success and is a significant step toward fully realizing MO routers on a chip.

Left: Wave propagation at the top of a dual waveguide and coupler at 1550 nm. Right: Mode profile of a coupler and dual waveguide. Copyright © John Pritchard.

Investigating the Effect of MO Material and the Design of a Magnetic Field Generator

The coupler and waveguide designs we’ve discussed thus far are ideal for the single-mode confinement of light at 1550 nm. Now, let’s see how adding a top layer of MO material to the SOI rib waveguide affects the device. Specifically, the goal is to find out the amount of light that is exposed to the Faraday rotation. This indicates when light with a rotated state of polarization interferes with nonrotated light.

Mode analysis of an SOI waveguide with a top layer of MO material. Copyright © John Pritchard.

The results, highlighted above, show that the MO material contains 3.9% of the light. Despite being a small percentage, previous research suggests that this creates sufficient Faraday rotation to observe interference at the electrical output. But for this to happen, the material needs to be magnetized with a permanent magnet or controlled magnetic field generator. Finding appropriate monolithically integrated magnetic field generators was therefore a final point of consideration.

While magnetic field generation techniques are important for creating on-chip MO modulators, the process itself is complex. The small size of MO systems makes it difficult to develop monolithically integrated magnetic field generators. To address this, Pritchard used simulation to validate the design of a novel dynamic magnetic field generator: a four-turn integrated coil.

Left: Geometry of an integrated magnetic field generator. Right: Geometry of the integrated magnetic field generator with the MO material highlighted in pink and the silicon waveguide shown in purple. Copyright © John Pritchard.

The results show that the coil generated 260 G near the center of the optical waveguide when energized with a 35 mA current. Within the tested waveguide dimensions, this magnetic field strength can magnetize Ce:YIG film on silicon.

It is possible to expand such research by investigating the field at the center of the MO material, which is part of the core of the four-turn integrated coil. Here, the simulation studies indicate that with a current of 35 mA, the magnetic field at the center of the MO material layer has a maximum field of about 210 G, a reduction possibly explained by the difference in properties of the material. Such findings speak to the potential of on-chip MO routing solutions and can be used as a resource in improving their design and manufacturing processes.

Simulation results for the magnetic field generator at the center of the coil. Copyright © John Pritchard.

Simulation Sheds Light on the Future of Optical Research

Future on-chip optical network architects will have a variety of active switching and routing options, allowing them to make their networks more robust by using both EO and MO devices. While it’s important to note that the results mentioned here are preliminary and more research is needed, the simulations and design methodologies act as a proof of concept for on-chip magnetic field generators and silicon rib waveguides. They can serve as a useful foundation for continued studies on such devices, creating a path for furthering their optimization.

As John Pritchard notes: “Some of the most beautiful connections between light, magnetism, and quantum theory have led to breathtaking technologies ranging from superconductor imaging to gigawatt laser pulses. These have enabled revolutionary inventions in transportation; measurement instruments used to understand the birth of the universe; and, in the near future, optical integrated circuits.” Looking to the future, we are eager to see the continued role of multiphysics simulation in advancing optical research, a field with wide-reaching applications.

Read More About Wave Optics Modeling

• Read the article that inspired this blog post in Magnetics Technology International 2016: “Magneto-optic router on a chip”
• Browse the Wave Optics category on the COMSOL Blog

We previously learned how to calculate the Fourier transform of a rectangular aperture in a Fraunhofer diffraction model in the COMSOL Multiphysics® software. In that example, the aperture was given as an analytical function. The procedure is a bit different if the source data for the Fourier transformation is a computed solution. In this blog post, we will learn how to implement the Fourier transformation for computed solutions with an electromagnetic simulation of a Fresnel lens.

Fourier Transformation with Fourier Optics

Implementing the Fourier transformation in a simulation can be useful in Fourier optics, signal processing (for use in frequency pattern extraction), and noise reduction and filtering via image processing. In Fourier optics, the Fresnel approximation is one of the approximation methods used for calculating the field near the diffracting aperture. Suppose a diffracting aperture is located in the plane at . The diffracted electric field in the plane at the distance from the diffracting aperture is calculated as

where, is the wavelength and account for the electric field at the plane and the plane, respectively. (See Ref. 1 for more details.)

In this approximation formula, the diffracted field is calculated by Fourier transforming the incident field multiplied by the quadratic phase function .

The sign convention of the phase function must follow the sign convention of the time dependence of the fields. In COMSOL Multiphysics, the time dependence of the electromagnetic fields is of the form . So, the sign of the quadratic phase function is negative.

Fresnel Lenses

Now, let’s take a look at an example of a Fresnel lens. A Fresnel lens is a regular plano-convex lens except for its curved surface, which is folded toward the flat side at every multiple of along the lens height, where m is an integer and n is the refractive index of the lens material. This is called an m^th-order Fresnel lens.

The shift of the surface by this particular height along the light propagation direction only changes the phase of the light by (roughly speaking and under the paraxial approximation). Because of this, the folded lens fundamentally reproduces the same wavefront in the far field and behaves like the original unfolded lens. The main difference is the diffraction effect. Regular lenses basically don’t show any diffraction (if there is no vignetting by a hard aperture), while Fresnel lenses always show small diffraction patterns around the main spot due to the surface discontinuities and internal reflections.

When a Fresnel lens is designed digitally, the lens surface is made up of discrete layers, giving it a staircase-like appearance. This is called a multilevel Fresnel lens. Due to the flat part of the steps, the diffraction pattern of a multilevel Fresnel lens typically includes a zeroth-order background in addition to the higher-order diffraction.

A Fresnel lens in a lighthouse in Boston. Image by Manfred Schmidt — Own work. Licensed under CC BY-SA 4.0, via Wikimedia Commons.

Why are we using a Fresnel lens as our example? The reason is similar to why lighthouses use Fresnel lenses in their operations. A Fresnel lens is folded into in height. It can be extremely thin and therefore of less weight and volume, which is beneficial for the optics of lighthouses compared to a large, heavy, and thick lens of the conventional refractive type. Likewise, for our purposes, Fresnel lenses can be easier to simulate in COMSOL Multiphysics and the add-on Wave Optics Module because the number of elements are manageable.

Modeling a Focusing Fresnel Lens in COMSOL Multiphysics®

The figure below depicts the optics layout that we are trying to simulate to demonstrate how we can implement the Fourier transformation, applied to a computed solution solved for by the Wave Optics, Frequency Domain interface.

Focusing 16-level Fresnel lens model.

This is a first-order Fresnel lens with surfaces that are digitized in 16 levels. A plane wave is incident on the incidence plane. At the exit plane at , the field is diffracted by the Fresnel lens to be . This process can be easily modeled and simulated by the Wave Optics, Frequency Domain interface. Then, we calculate the field at the focal plane at by applying the Fourier transformation in the Fresnel approximation, as described above.

The figures below are the result of our computation, with the electric field component in the domains (top) and on the boundary corresponding to the exit plane (bottom). Note that the geometry is not drawn to scale in the vertical axis. We can clearly see the positively curved wavefront from the center and from every air gap between the saw teeth. Note that the reflection from the lens surfaces leads to some small interferences in the domain field result and ripples in the boundary field result. This is because there is no antireflective coating modeled here.

The computed electric field component in the Fresnel lens and surrounding air domains (vertical axis is not to scale).

The computed electric field component at the exit plane.

Implementing the Fourier Transformation from a Computed Solution

Let’s move on to the Fourier transformation. In the previous example of an analytical function, we prepared two data sets: one for the source space and one for the Fourier space. The parameter names that were defined in the Settings window of the data set were the spatial coordinates in the source plane and the spatial coordinates in the image plane.

In today’s example, the source space is already created in the computed data set, Study 1/Solution 1 (sol1){dset1}, with the computed solutions. All we need to do is create a one-dimensional data set, Grid1D {grid1}, with parameters for the Fourier space; i.e., the spatial coordinate in the focal plane. We then relate it to the source data set, as seen in the figure below. Then, we define an integration operator intop1 on the exit plane.

Settings for the data set for the transformation.

The intop1 operator defined on the exit plane (vertical axis is not to scale).

Finally, we define the Fourier transformation in a 1D plot, shown below. It’s important to specify the data set we previously created for the transformation and to let COMSOL Multiphysics know that is the destination independent variable by using the dest operator.

Settings for the Fourier transformation in a 1D plot.

The end result is shown in the following plot. This is a typical image of the focused beam through a multilevel Fresnel lens in the focal plane (see Ref. 2). There is the main spot by the first-order diffraction in the center and a weaker background caused by the zeroth-order (nondiffracted) and higher-order diffractions.

Electric field norm plot of the focused beam through a 16-level Fresnel lens.

Concluding Remarks

In this blog post, we learned how to implement the Fourier transformation for computed solutions. This functionality is useful for long-distance propagation calculation in COMSOL Multiphysics and extends electromagnetic simulation to Fourier optics.

Read More About Simulating Wave Optics

• Simulating Holographic Data Storage in COMSOL Multiphysics
• How to Simulate a Holographic Page Data Storage System
• How to Implement the Fourier Transformation in COMSOL Multiphysics

References

1. J.W. Goodman, Introduction to Fourier Optics, The McGraw-Hill Company, Inc.
2. D. C. O’Shea, Diffractive Optics, SPIE Press.

Optical fibers that deliver midinfrared wavelengths are in high demand for a range of relative applications. As infrared transparent materials, semiconductors are useful for this purpose when combined with silica, helping to realize a new generation of midinfrared fiber optics. While important to performance, measuring the optical losses of such structures can be challenging experimentally because of time and costs. Simulation enables us to efficiently model this behavior for varying wavelengths and fiber geometries and identify strategies to reduce losses.

Semiconductors Help Advance the Design of Optical Fibers

Sensors, chemical imaging, and optoelectronics: These are just some of the applications in which midinfrared wavelengths are of significance. With their growing importance across various industries and technologies, the need for identifying optical fibers that can produce midinfrared light in a large wavelength range is increasing as well.

One approach is to fuse silica — a typical material for optical fibers — with infrared transparent semiconductors like germanium, zinc selenide, and silicon. To be more specific, silica makes up the cladding, or outer layer, of the optical fiber design and the selected semiconductor makes up its core. This combination provides opportunities for developing new types of midinfrared multimaterial optical fibers.

A multimaterial optical fiber design. Image by X. Ji, R. Page, and V. Gopalan and taken from their COMSOL Conference 2016 Boston paper.

In order for these optical fiber designs to be effective, an important step is to better understand their optical losses. While this can be time consuming and costly via experiments, simulation tools like the COMSOL Multiphysics® software provide a more efficient route for modeling this behavior and identifying means of optimization. Let’s look at an example from researchers at Pennsylvania State University and Pacific Lutheran University that involves the analysis and design of a germanium-based optical fiber.

Measuring Propagation Losses in a Germanium-Based Optical Fiber

For their analysis, the researchers used the RF Module, an add-on product to COMSOL Multiphysics. After defining their respective geometries, they applied refractive indices to both the core and cladding of the optical fiber at a particular wavelength. Along the outside of the cladding, the electric field is said to be zero. The plot below shows the electric field distribution for a characteristic HE₁₁ mode that is confined and guided through a 6-μm core diameter made of germanium.

The electric field distribution of a characteristic HE₁₁ mode within the core diameter. Image by X. Ji, R. Page, and V. Gopalan and taken from their COMSOL Conference 2016 Boston paper.

To identify the optimal fiber geometry and operative wavelength range, the research team simulated the mode’s propagation attenuation as a function of wavelength and core diameter. Between 2 and 4 μm, a window of low optical loss occurs. As the wavelength becomes longer, the loss begins to increase. This is due to the evanescent wave extending further into the cladding region and the increase in silica’s extinction coefficient at a longer wavelength. Note that the loss related to this effect is larger when the core diameter is smaller.

Left: The optical losses for the fibers. Right: The electric field distributions of the HE₁₁ mode in the core diameter for varying wavelengths. Images by X. Ji, R. Page, and V. Gopalan and taken from their COMSOL Conference 2016 Boston paper.

For these longer wavelengths, one strategy for reducing optical loss and achieving a wider window of high transmission is to add another layer of material between the germanium and silica. This material needs to have smaller refractive indices than germanium and a smaller extinction coefficient than silica over a large wavelength range. Two good candidates for this are silicon and zinc selenide. In the plot below, we can see the characteristic HE₁₁ mode confined and guided through each of these new fiber structures.

The electric field distribution of a characteristic HE₁₁ mode within the core diameter when an interfacial layer is added. Image by X. Ji, R. Page, and V. Gopalan and taken from their COMSOL Conference 2016 Boston paper.

Once again, the researchers simulated the optical loss as a function of the wavelength for a 6-μm core diameter. As the results indicate, introducing the additional layer significantly reduces the optical propagation losses, particularly at longer wavelengths. What’s more: It does so without having to sacrifice the size of the core diameter.

Left: The optical losses for the fibers that include an added layer. Right: The electric field distributions of the HE₁₁ mode in the core diameter at a wavelength of 10 μm. Images by X. Ji, R. Page, and V. Gopalan and taken from their COMSOL Conference 2016 Boston paper.

From the above results, it is clear that the reduction in optical loss is more pronounced in the zinc selenide case. This is because the refractive index between germanium and zinc selenide is greater than that between germanium and silicon, allowing light to be better confined. However, smaller refractive index differences often reduce the constraint of a small core diameter for single-mode guidance.

To account for this, the researchers calculated the single-mode guidance for each germanium-based core diameter configuration. The results show that the zinc selenide structure requires a smaller germanium core diameter to achieve single-mode guidance.

The germanium-based core diameter requirements for the zinc selenide (a) and silicon (b) structures. The gray areas represent conditions for single-mode guidance. Image by X. Ji, R. Page, and V. Gopalan and taken from their COMSOL Conference 2016 Boston paper.

Simulation Fosters the Design of a New Generation of Midinfrared Fiber Optics

With the flexibility of COMSOL Multiphysics, the research team was able to easily modify different parameters in their optical fiber design and analyze the impact on fiber performance. From there, they implemented further strategies to minimize optical losses and enable greater transmission. Their optimized fiber design has potential use in the medical field, specifically in endoscopes for spectroscopic imaging.

Resources for Modeling Optical Fibers in COMSOL Multiphysics®

• Read the full COMSOL Conference paper: “Design of Next Generation Mid-infrared Fiber Optics“
• Download related examples from our Application Gallery:
  • Stress-Optical Effects with Generalized Plane Strain
  • Step-Index Fiber Bend
  • Fiber Simulator

Whenever light is incident on a dielectric material, like glass, part of the light is transmitted while another part is reflected. Sometimes, we add a metal coating, such as gold, which alters the transmittance and reflectance as well as leads to some absorption of light. The dielectric surface and the metal coating also often have some random variations in height and thickness. In this blog post, we will introduce and develop a computational model for this situation.

Starting Simple: An Optically Flat Surface

Before we get to the rough surface, let’s start with something simple: a thin uniform layer of gold coating on top of optically flat glass, as shown in the image below. Such a model exhibits negligible structural variation in the plane of glass. In addition, it can be modeled quite simply in the COMSOL Multiphysics® software by considering a small two-dimensional unit cell that has a width much smaller than the wavelength.

This computational model is based on the Fresnel equation example, one of the verification models in the Application Gallery, but is modified to include a layer of gold with a wavelength-dependent refractive index. This type of index requires that we manually adjust the mesh size based on the minimum wavelength in each material as well as the skin depth, as described in a previous blog post.

Light incident on a metal coating on top of a glass substrate is reflected, transmitted, and absorbed.

The model includes Floquet periodic boundary conditions on the left and right sides of the modeling domain and a Port boundary condition at the top and bottom. The Port boundary condition at the top launches a plane wave at a specified angle of incidence and computes the reflected light, while the one at the bottom calculates the transmitted light. We can integrate the losses within the metal layer to compute the absorbance within the gold layer.

The computational model that calculates the optical properties of a metal film on glass.

If we are interested in computing incident light at off-normal incident angles, then we also have to concern ourselves with the height of the modeling domain — the distance between the material interfaces and the Port boundary conditions. This distance must be large enough such that any evanescent field drops off to approximately zero within the modeling domain.

The reason for this has to do with the Port boundary conditions, which can only consider the propagating component of the electromagnetic field. Any evanescent component of the field that reaches the Port boundary condition is artificially reflected, so we must place the port boundary far enough away from the material interfaces. In the most general cases, it is difficult to determine how far the evanescent field extends. A simple rule of thumb is to place the Port boundary conditions at least half a wavelength away from the material interfaces and to check if making the domain larger alters the results.

The sample results below show the transmitted, reflected, and absorbed light as well as their total — which should always add up to one. If these do not add up to one, then we must carefully check our model setup.

The transmittance, reflectance, and absorbance of light normally incident on a flat glass surface with a metal coating as a function of wavelength.

The transmittance, reflectance, and absorbance of 550-nm light at various angles of incidence.

Adding Complexity: A Surface with Periodic Variations

Let’s now make things a little bit more complicated and introduce a periodic structural variation: a sinusoidal ripple. Clearly, we now need to consider a larger unit cell that considers a single ripple.

A surface with periodic variations reflects and transmits light into several different diffraction orders.

We can still apply the same domain properties and all of the same boundary conditions. However, if spacing is large enough, then we can have higher-order diffraction. In other words, light can be reflected and transmitted into several different directions. To properly compute the reflection and transmission, we need to add several diffraction order ports. The software computes the appropriate number of ports based on the domain width, material properties, and specified incident angle. If we are studying a range of incident angles, we must make sure to compute all of the diffraction orders present at the limits of the angular sweep.

There can be multiple diffraction orders present, depending on the ratio of wavelength to domain width, refractive index, and incident angles.

The conditions under which higher-order diffraction appears and the appropriate modeling procedure is presented in depth in the example of a plasmonic wire grating, so let’s not go into it at length here. In short, the wider the computational domain relative to the wavelengths in the materials above and below, the more diffraction orders can be present (the number of diffraction orders varies with the incident angle). The results shown below plot the total transmittance and reflectance; i.e., all of the light reflected into the different diffraction orders is added up, as is all of the transmitted light.

The transmittance, reflectance, and absorbance of light normally incident on a rippled glass surface with a metal coating.

The transmittance, reflectance, and absorbance of 550-nm light at various angles of incidence.

Solving a More Difficult Case: A Surface with Random Roughness

Let’s now move on to the most computationally difficult case: a surface with many random variations in the surface height. To model the randomness, we must model several different domains of increasing widths and different subsets of the rough profile. As the domain width increases — and as different subsets of the surface are sampled — the average behavior computed from these different models converges. That is, we generate a set of statistics by sampling the rough surface. Rather than going into detail on how to calculate these statistics, let’s focus on how to model one domain that approximates a rough surface by defining the height variation as the sum of different sinusoids with random height and phase, as described here.

A rough surface with random variations reflects and transmits light in random directions. The computational model must sample a statistically significant subset of the roughness profile.

Our computational domain must now be very wide, many times longer than the wavelength. As we still want to model a plane wave incident at various angles on the structure, we use the Floquet periodic boundary conditions, which require that we have an identical mesh on the periodic boundaries. Practically speaking, this means that we may need to slightly alter the geometry of our domain to ensure that the boundaries on the left and right side are identical. If we do use a sum of sine functions, as described here, then the profile will automatically be periodic.

We still want to launch the wave with a Port boundary condition. However, it is no longer practical to use diffraction order ports to monitor the reflected and transmitted light, as this can result in hundreds (or thousands) of diffraction orders. Furthermore, since this model represents a statistical sampling, the relative fraction of light scattered into these different orders is not of interest; we’re only interested in the sum of the total reflected and transmitted light. That is, this modeling approach computes the total integrated scatter plus the specular reflection and transmission of the surface.

The computational domain for a model of a rough surface. Light is launched from the interior port toward the material interface. Light reflected back toward this port passes though it and is absorbed in the PML, as is the transmitted light. Two additional boundaries are introduced to monitor the total reflectance and transmittance.

Thus, we introduce an alternative modeling strategy that does not use ports to compute reflection and transmission. Instead, we use a perfectly matched layer (PML) above and below to absorb all reflected and transmitted light as well as probes to compute reflection and transmission. PMLs absorb any fields incident upon them, as described in this blog post on using PMLs for wave electromagnetics problems.

The PML absorbs both propagating and evanescent components of the field, but we only want it to absorb the propagating component. Thus, we again need to ensure that we place the PMLs far enough away from the material interfaces. We use the same rule of thumb as before, placing the PML at least half a wavelength away from the material interfaces.

As we approach grazing angles of incidence, even the PML domain does not, by default, absorb all of the light. At nearly grazing angles, the effective wavelength in the absorbing direction is very long, and we need to modify the default wavelength in the PML settings (shown below). This change to the settings is only necessary if we are interested in angles of incidence greater than ~75°.

The PML settings modified to account for grazing angles of incidence.

Since our domain is now bounded by PMLs above and below, the port that launches the wave must now be placed within the modeling domain. To do this, we use the Slit Condition option to define an interior port that is backed by a domain. This means that the port now launches a wave in one direction, emanating from this interior boundary. Any light reflected back toward the boundary passes through unimpeded and then gets absorbed by the PML.

Although this is a good way to launch the wave, we will no longer use the Port boundary condition to compute how much light is reflected, since we would have to add hundreds of diffraction ports, and similarly, we’d need hundreds of ports to compute the total transmittance.

To monitor the total transmitted and reflected light, we instead introduce two additional interior boundaries to the model, placed just in front of the PML domains (shown in the schematic above). At these two boundaries, we integrate the power flux in the upward and downward directions, normalized by the incident power, which gives us the total reflectance and transmittance. To more accurately determine the integral of the power flux at these boundaries, we also introduce a boundary layer mesh composed of a single layer of elements much smaller than the wavelength.

On the incident side, we place this monitoring boundary above the interior port. The launching port introduces a plane wave propagating toward the material interface. The light reflected at the interface passes through this interior port, then moves through the boundary at which we monitor reflectance, and is absorbed in the PML.

The plots below show sample results of the transmittance, reflectance, and absorbance. They are notably different from the smooth surface and periodically varying surface results. Note that the sweep over the angle of incidence terminates at 85° off normal. Of course these plots will look slightly different for each different random geometry case that we run.

The transmittance, reflectance, and absorbance of light normally incident on a rough glass surface.

The transmittance, reflectance, and absorbance of 550-nm light at angles of incidence up to 85° off normal.

Concluding Thoughts on Calculating the Optical Properties of Rough Surfaces

Here, we have introduced a modeling approach that is appropriate for computing the optical transmission and reflection from a rough surface. This method contrasts with the approach for modeling a uniform optically flat surface as well as the one for modeling surfaces with periodic variations. The modeling method for rough surfaces can also be used for the modeling of periodic structures that have a very long period, such as when the scattering into different diffraction orders is not of interest.

Modeling truly random surfaces does require some care, as the geometry needs to be altered to ensure that it is periodic. Furthermore, the domain size and number of different random geometries studied must be large enough to give statistically meaningful results. Since this requires solving many different variations of the same model and postprocessing the results, it is helpful to use the Application Builder, LiveLink™ for MATLAB®, or LiveLink™ for Excel® in our modeling workflow.

Further Resources

• See how to create a rough surface as a sum of sine functions
• See how to create a random geometry using model methods
• Check out other blog posts related to simulating wave optics:
  • Modeling of Materials in Wave Electromagnetics Problems
  • Modeling of Metallic Objects in Wave Electromagnetics

MATLAB is a registered trademark of The MathWorks, Inc. Microsoft and Excel are either registered trademarks or trademarks of Microsoft Corporation in the United States and/or other countries.

In 1870, an audience watched as a stage was set with two buckets, one on top of the other. Due to a small hole in the upper bucket, water poured into the lower bucket, bending as it did so. To the audience’s amazement, sunlight followed the bend of water — a phenomenon later termed total internal reflection. The performer on stage, John Tyndall, was one of the many scientists who tried to control the most visible form of energy: light.

Entering the Era of Photonics

For decades, researchers aimed to find a way to control light and use it for the transmission and processing of information, an area of study known as photonics. In the meantime, electrons took this responsibility on their shoulders. More recently, scientists were able to viably manufacture nanostructure devices and control the flow of light, due to the extensive development of technologies such as photolithography, molecular beam epitaxy, and chemical vapor deposition. The packets of light (photons) were projected as a prospective candidate to assume the responsibilities of sustaining Moore’s law.

The Beginning of the Photonic Integrated Circuit

The goal of researchers studying photonics was to deliver an analogue of an electronic integrated chip that could perform all of the required computational processes using photons while being space and time efficient. Scientists termed this technology photonic integrated circuit (PIC), devices that could integrate different optical components on a single substrate. This chip should, in principle, be able to perform various optical operations, such as focusing, splitting, isolation, polarization, coupling, modulation, and (eventually) detecting light.

Schematic of the photonic integrated circuit (not to scale), showcasing different optical components. For more information, see Ref. 1.

In this blog post, which is the first in a new series, we discuss optical waveguides. Later in the blog series, we will contemplate how these optical components came to be an inevitable part of PICs.

Developing Optical Components for PICs

The different optical components constituting a fully functioning PIC were subject to research. Scientists determined that the way to create the light source was through lasers, which could deliver a narrow-band light source to the integrated chip component. As for optical fibers, they could transport light from one end to the other for thousands of kilometers. Then there was the most common component in a PIC: the optical waveguide. This waveguide could link different components on the substrate.

Input couplers were developed to efficiently couple the light from lasers or optical fibers to the optical waveguide placed on the substrate, while directional couplers were created to control the coupling of light between two parallel optical waveguides. Then came the ring resonator, which served the same purpose as an optical filter (that is, allowing only a narrow band of frequency) and could also couple two optical waveguides in opposite directions.

An example of an optical ring resonator notch filter.

Negotiating Nonlinear Effects

Some scientists probed the much underappreciated nonlinear optical effects to devise second-harmonic and third-harmonic waves. With these waves, it would be possible to perform operations between two optical beams, such as frequency doubling, differencing, and mixing.

Another invention was optical modulators. These components could modify the light intensity based on the applied DC bias potential using the nonlinear electro-optic effects.

Photonic Crystals: Controlling the Flow of Light

From nature, it was observed that with the periodic arrangement of high- and low-refractive-index materials in 1D, 2D, and 3D, it was possible to reflect a certain band of frequency while allowing another band of frequency to pass. Hence, these materials could act as both a filter and resonator in a certain periodic arrangement. The periodic arrangement of different dielectric materials was termed a photonic crystal.

Finding a Material to Propagate Light

With the idea of creating optical waveguides to propagate light on chip-scale packages, scientists were left to wonder which materials to use. One of the materials was high-refractive-index GaAs. This was used as the core and was surrounded by low-refractive-index AlGaAs. More advanced techniques were developed to dope titanium in the lithium niobate substrate to increase its refractive index and form a core.

The focus was narrowed down to silica, which is more easily available than any other material. The technology came to be known as silica on silicon (Si-SiO2) or silicon on insulator (SOI), where the silicon (high refractive index of ~3.5) was embedded within silica (lower refractive index of ~1.4). The fabrication techniques for silicon were well established (courtesy of electronic chips) and at the same time, silicon was compatible with other CMOS techniques, which helped boost research into silicon photonics technology.

Different Configurations of Silicon Waveguides

The crux of the silicon waveguide lies with the high contrast of the refractive index, around a 50% difference. Prior work relied on total internal reflection to confine the energy. In this case, energy was confined in a higher-refractive-index core that was surrounded by a low-refractive-index cladding. However, recent work confined the energy in the lower-refractive-index slot neighbored by the high-refractive-index slabs, inherently helping to lower losses.

Guiding Light in a High Refractive Index

The first technique involved confining the energy in a higher-refractive-index medium, where the inner core (in the order of hundreds of nanometers) is devised with a high-refractive-index material (silicon) surrounded by a low-refractive-index cladding (silica). The difference in the refractive index must be as much as 50%.

The fundamental mode is confined in the core, as shown in the image below on the left, and the confined normalized power, as shown in the image below on the right.

Left: The fundamental mode for an operating wavelength of 1.55 um. The white and black arrows depict the magnetic and electric field. Right: The normalized power density through the center of the waveguide.

Guiding Light in a Low Refractive Index

Although counterintuitive, the energy could also be trapped in a low refractive index. Moreover, it was found that more energy stays put in an even and narrow region (20 to 80 nm), which makes a low refractive index more compatible for integration with photonic circuits.

Such a design involves two slabs of high refractive index neighboring a nanoslot of low refractive index. Further, considerable energy is bounded in the slot.

Left: The transverse (Ex) field for a slot width of 50 nm. Right: The normalized transverse electric field (Ex) through the center of the waveguide.

To analyze the required width of the nanoslot for delivering maximum power through the waveguide, it was imperative to perform a sweep of the width, as shown below.

The normalized power and intensity in the slot versus slot width.

Designing and Prototyping Silicon Waveguides

Fabricating such an optical waveguide prototype and then analyzing it is resource intensive. An alternate, preferred approach is to use numerical tools such as the COMSOL Multiphysics® software. With this simulation tool, one could quickly set up prototypes and investigate further before finalizing the prototype to be fabricated.

We can use COMSOL Multiphysics to perform a mode analysis on the 2D cross section of the silicon waveguide (both for high- and low-refractive-index cases). This enables us to evaluate the effective refractive index of the waveguide and the fundamental mode, which helps us understand the normalized power distribution.

We implement the full 3D propagation for both types of waveguides by first having a 3D geometry of the optical waveguide and assigning Numeric Port boundary conditions on both ends of the waveguide. The Boundary Mode Analysis study (similar to a mode analysis in 2D) could be applied on these numeric ports to figure out their fundamental mode. The fundamental mode could be used to propagate within the waveguide using the Frequency Domain study, as shown in the animations below.

The y-component of the H-field propagating in the high-refractive-index confinement case for a silicon waveguide with a length of 10 um.

The y-component of the E-field propagating in the low-refractive-index confinement case for a silicon waveguide with a length of 10 um.

Final Thoughts on Silicon Waveguides

This is the first blog post in the Silicon Photonics blog series, where we will discuss different optical components in detail and how a finite element analysis tool such as COMSOL Multiphysics can help design these components. On our journey from laser cavities to photodetectors, we will meet some fascinating scientists and discuss how they attempted to control light.

Stay tuned!

References

1. B.E.A. Saleh and M.C. Teich, Fundamentals of Photonics.
2. K. Yamada, “Silicon Photonic Wire Waveguides: Fundamentals and Applications”, in Silicon Photonics II, 2011.
3. V. Almeida, Q. Xu, C. Barrios, and M. Lipson, “Guiding and confining light in void nanostructure”, Optics Letters, vol. 29, pp. 1209–1211, 2004.

On a bright evening in 1669, Professor Erasmus Bartholinus looked through a piece of an Icelandic calcite crystal he had placed onto a bench. He observed when he covered text on the bench with the stone, it appeared as a double image. The observed optical phenomenon, called birefringence, involves a beam of light that splits into two parallel beams while emerging out of a crystal. Here, we demonstrate a modeling approach for this effect.

Understanding Anisotropic Materials

The beam of light that Erasmus Bartholinus observed traveling straight through the crystal is called an ordinary ray. The other light beam, which bends while traveling through the crystal, is an extraordinary ray. Anisotropic materials, such as the crystal from the stone and bench experiment described above, are found in applications ranging from detecting harmful gases to beam splitting for photonic integrated circuits.

Ordinary and extraordinary rays traveling through an anisotropic crystal.

In a physical context, when an unpolarized electromagnetic beam of light propagates through an anisotropic dielectric material, it polarizes the dielectric domain, leading to a distribution of charges known as electric dipoles. This phenomenon leads to induced fields within the anisotropic dielectric material, wherein two kinds of waves experience two different refractive indices (ordinary and extraordinary).

The ordinary wave is polarized perpendicular to the principal plane and the extraordinary wave is polarized parallel to the principle plane, where the principal plane is spanned by the optic axis and the two propagation directions in the crystal. Because of this behavior, the waves propagate with different velocities and trajectories.

Introducing Anisotropy Within Silicon Waveguides

In a previous blog post, we discussed silicon and how its derivative, silicon dioxide, is used extensively in photonic integrated chips due to its compatibility with the CMOS fabrication technique. Bulk silicon, which has an isotropic property, is used to develop prototypes for photonic integrated chips. However, due to unique optical properties such as splitting beams and polarization-based optical effects, anisotropy comes into play at a later stage.

Anisotropy in silicon photonics occurs unintentionally due to the annealing process while fabricating the waveguide. The difference in thermal expansion between the core and cladding causes geometry mismatch due to stress optical effects, which results in effects such as mode splitting and pulse broadening. Anisotropy could also be intentionally introduced by varying the porosity of silicon dioxide. This enables researchers to work with a range of effective refractive indices from silicon dioxide (n ~1.44) to air (n ~1), giving them the edge to perform very sensitive optical sensor applications.

Optical Modes of Propagation

To perform qualitative analyses of anisotropic media, researchers investigate how optical energy propagates within planar waveguides (also known as modes of propagation). In planar waveguides, we define modes using and terminology (Ref. 2), where x and y depict the direction of polarization and p and q depict the number of maxima in the x- and y-coordinates.

Picture it this way: You are walking on an “landscape” (as shown below). The “winds” (polarization) are along ±x direction, and you encounter two distinct peaks when traveling from the -x to +x direction. When you move from the -y to +y direction, you observe both of the peaks simultaneously.

Mode analysis of the planar waveguide. Top row, left to right: and . Middle row, left to right: and . Bottom row, left to right: and . The arrow plot represents the electric field; contour and surface plot represent out-of-plane power flow (red is high and blue is low magnitude).

Analyzing Anisotropic Structures in the COMSOL Multiphysics® Software

Before launching a beam of light through a waveguide using a laser source, it is important to know which optical modes could persist within a specified core/cladding dimension of the waveguide. Performing a mode analysis using a full vectorial finite element tool, such as the COMSOL Multiphysics® software, could be very helpful to qualitatively and quantitatively analyze the optical modes and dispersion curve respectively.

Introducing Diagonal Anisotropy

Performing a modal analysis on any isotropic material requires the definition of a single complex value, while in the case of an anisotropic material, a full tensor relative permittivity approach is required. The electric permittivity essentially relates the electric field with the material property. Here, tensor refers to a 3-by-3 matrix that has both diagonal (_xx, _yy, _zz) and off-diagonal (_xy, _xz, _yx, _yz, _zx, _zy) terms as shown below.

However, for all materials, you can find a coordinate system in which you only have nonzero diagonal elements in the permittivity tensor, whereas the off-diagonal elements are all zero. The three coordinate axes in this rotated coordinate system are the principal axes of the material and, correspondingly, the three values for the diagonal elements in the permittivity tensor are called the principal permittivities of the material.

There are basically two kinds of anisotropic crystal: uniaxial and biaxial crystal. With a suitable choice of coordinate system, where only the diagonal elements of the permittivity tensor are nonzero, in terms of optical properties, uniaxial crystal considers only the diagonal terms, that is _xx = _yy = (n_o)², _zz = (n_e)², where n_o and n_e are the ordinary and extraordinary refractive indices. However, when , it is known as a biaxial crystal.

To put this argument into a modeling perspective, we can extend the buried rib waveguide example from this blog post on silicon photonics design. We can perform a modal analysis on the 2D cross section of the waveguide with the square core and cladding length of 4 um and 20 um, respectively (shown below). The operating wavelength for all the cases is considered as 1.55[um].

Schematic of 3D buried rib optical waveguide where the mode analysis was performed at the inlet 2D cross section. The intensity plot and arrow plot representing the mode and polarization of E-fields respectively.

Core of the rib waveguide depicting the optic axis (red) along the x-axis and the principal axis (blue).

In the classic case of a uniaxial material, we assume the optic axis (i.e., c-axis) is along the principal x-axis (as shown above) and consider the diagonal relative permittivity _yy and _zz terms (which are orthogonal to the c-axis) as the square of ordinary refractive index (~1.5199² ~ 2.31). The _xx component element that is along the c-axis is considered as the square of extraordinary refractive index (~1.4799² ~ 2.19) (as per Ref. 3). In addition, the off-diagonal terms are considered zero (as shown below) and the cladding has an isotropic relative permittivity (~1.4318²). The optical modes derived are the 6 modes shown above. Note the difference in the refractive indices: “n_xx – n_yy” is known as birefringence, where n_xx = and n_yy = .

Relative permittivity tensor with diagonal elements.

Dispersion Curves

By evaluating the optical modes, we can visually comprehend the behavior of the optical waveguide. However, the dispersion curves could also be handy for performing quantitative analyses. A dispersion curve represents the variation of the effective refractive index with respect to the length of the waveguide or the operating frequency.

Diagonal Anisotropy

A modal analysis is performed while parametrically sweeping the length of the waveguide from 0.5 um to 4 um to derive the dispersion curve for the anisotropic core, as shown in the figure below. We assume the earlier case stated, with diagonal anisotropy terms of the core (i.e., _xx = 2.19, _yy = _zz = 2.31 and all of the diagonal elements are zero). The results are compared with Koshiba et al. (Ref. 3).

Dispersion curve with transverse anisotropic core.

Off-Diagonal Transverse Anisotropy (XY Plane)

When the optic axis (i.e., c-axis) lies in XY plane and makes an angle of with the x-axis, the diagonal components _xx, _yy, _zz and off-diagonal components _xy and _yz are nonzero, while the rest of the components are zero. The full relative permittivity tensor could be evaluated by using the rotation matrix [R] as shown below, where the rotation matrix [R] is specifically for rotating the c-axis in the XY plane. _xx is the square of the extraordinary refractive index (~2.19), because the c-axis lies along the principal x-axis, while _yy and _zz are the square of the ordinary refractive index (~2.31). The off-diagonal elements _xy and _yz are derived from the multiplication of the matrices as stated below.

The c-axis lying in the XY plane and making an angle of with the x-axis.

The relative permittivity tensor ε is treated along with a rotation matrix, rotating the c-axis in the XY plane with angle .

Finally, the modal analysis of the waveguide with off-diagonal anisotropic core and isotropic cladding, where the optic axis makes angles of 0, 15, 30, and 45 degrees with respect to the principal x-axis, as shown below. Here, it could be observed that the direction of the in-plane magnetic field changes according to the change in the angle of the optic axis. The dispersion curve could also be plotted by parametrically sweeping the length of the core and cladding from 0.5 um to 4 um, while considering the angle as 45°. The dispersion curve tends to be similar to the dispersion curve of the diagonal anisotropy, as discussed above.

Mode analysis, including off-diagonal terms, for θ = 0° (top-left), θ = 15° (top-right), θ = 30° (bottom-left), and θ = 45° (bottom-right). The figure represents the magnetic field lines within the core for different rotation angles.

Off-Diagonal Longitudinal Anisotropy (YZ Plane)

Finally, when considering the longitudinal anisotropy where the optic axis (i.e., c-axis) lies in the YZ plane and makes an angle of with the y-axis, the diagonal components _xx, _yy, _zz and the off-diagonal components _yz and _zy are nonzero, while the rest of the components are zero. The relative permittivity tensor could be evaluated by using the rotation matrix [R] as shown below, where the rotation matrix [R] is specifically for rotating the c-axis in the YZ plane. _yy is the square of the extraordinary refractive index (~2.19), because the c-axis lies along the principal y-axis, while _xx, _zz is the square of the ordinary refractive index (~2.31). The off-diagonal elements _yz and _zy are derived from the multiplication of the matrices as stated below.

The c-axis lying in the YZ plane and making an angle of with the x-axis.

The relative permittivity tensor ε is treated along with a rotation matrix, rotating in the YZ plane with angle .

A modal analysis is then performed where the length of the waveguide is parametrically swept from 0.5 um to 4 um to derive the dispersion curve for the longitudinal anisotropic core, as shown in the figure below. In this case, = 45° (i.e., the c-axis lies in the YZ plane and makes 45° with the y-axis) (Ref. 3).

Dispersion curve with longitudinal anisotropic core.

Final Thoughts on Modeling Anisotropic Materials

In this blog post, we performed qualitative analyses (modes of propagation) and quantitative analyses (dispersion curves) of the anisotropic optical waveguide using modal analysis in COMSOL Multiphysics. Diagonal anisotropy as well as off-diagonal transverse and longitudinal anisotropy were considered to derive their dispersion relationships. These types of analyses give us more flexibility when carrying out optimization of material and geometric parameters to help us gain an in-depth and intuitive understanding of the physics of anisotropic materials.

A simple tutorial model to help you started would be the Step-Index Fiber, which involves mode analysis over a 2D cross section of the 3D optical fiber.

References

1. E. Hecht, Optics, Pearson.
2. E.A.J. Marcatili, “Dielectric rectangular waveguide and directional coupler for integrated optics”, Bell Syst. Tech. J., vol. 48, pp. 2071–2102, 1969.
3. M. Koshiba, K. Hayata, and M. Suzuki, “Finite-element solution of anisotropic waveguides with arbitrary tensor permittivity,” Journal of Lightwave Technology, vol. 4, no. 2, pp. 121–126, 1986.

In the wave optics field, it is difficult to simulate large optical systems in a way that rigorously solves Maxwell’s equation. This is because the waves that appear in the system need to be resolved by a sufficiently fine mesh. The beam envelopes method in the COMSOL Multiphysics® software is one option for this purpose. In this blog post, we discuss how to use the Electromagnetic Waves, Beam Envelopes interface and handle its restrictions.

Comparing Methods for Solving Large Wave Optics Models

In electromagnetic simulations, the wavelength always needs be resolved by the mesh in order to find an accurate solution of Maxwell’s equations. This requirement makes it difficult to simulate models that are large compared to the wavelength. There are several methods for stationary wave optics problems that can handle large models. These methods include the so-called diffraction formulas, such as the Fraunhofer, Fresnel-Kirchhoff, and Rayleigh-Sommerfeld diffraction formula and the beam propagation method (BPM), such as paraxial BPM and the angular spectrum method (Ref. 1).

Most of these methods use certain approximations to the Helmholtz equation. These methods can handle large models because they are based on the propagation method that solves for the field in a plane from a known field in another plane. So you don’t have to mesh the entire domain, you just need a 2D mesh for the desired plane.

Compared to these methods, the Electromagnetic Waves, Beam Envelopes interface in COMSOL Multiphysics (which we will refer to as the Beam Envelopes interface for the rest of the blog post) solves for the exact solution of the Helmholtz equation in a domain. It can handle large models; i.e., the meshing requirement can be significantly relaxed if a certain restriction is satisfied.

A beam envelopes simulation for a lens with a millimeter-range focal length for a 1-um wavelength beam.

We discuss the Beam Envelopes interface in more detail below.

Theory Behind the Beam Envelopes Interface

Let’s take a look at the math that the Beam Envelopes interface computes “under the hood”. If you add this interface to a model and click the Physics Interface node and change Type of phase specification to User defined, you’ll see the following in the Equation section:

Here, is the dependent variable that the interface solves for, called the envelope function.

In the phasor representation of a field, corresponds to the amplitude and to the phase, i.e.,

The first equation, the governing equation for the Beam Envelopes interface, can be derived by substituting the second definition of the electric field into the Helmholtz equation. If we know , the only unknown is and we can solve for it. The phase, , needs to be given a priori in order to solve the problem.

With the second equation, we assume a form such that the fast oscillation part, the phase, can be factored out from the field. If that’s true, the envelope is “slowly varying”, so we don’t need to resolve the wavelength. Instead, we only need to resolve the slow wave of the envelope. Because of this process, simulating large-scale wave optics problems is possible on personal computers.

A common question is: “When do you want the envelope rather than the field itself?” Lens simulation is one example. Sometimes you may need the intensity rather than the complex electric field. Actually, the square of the norm of the envelope gives the intensity. In such cases, it suffices to get the envelope function.

What Happens If the Phase Function Is Not Accurately Known?

The math behind the beam envelope method introduces more questions:

• What if the phase is not accurately known?
• Can we use the Beam Envelopes interface in such cases?
• Are the results correct?

To answer these questions, we need to do a little more math.

1D Example

Let’s take the simplest test case: a plane wave, , where for wavelength = 1 um, it propagates in a rectangular domain of 20 um length. (We intentionally use a short domain for illustrative purposes.)

The out-of-plane wave enters from the left boundary and transmits the right boundary without reflection. This can be simulated in the Beam Envelopes interface by adding a Matched boundary condition with excitation on the left and without excitation on the right, while adding a Perfect Magnetic Conductor boundary condition on the top and bottom (meaning we don’t care about the y direction).

The correct setting for the phase specification is shown in the figure below.

We have the answer , knowing that the correct phase function is or the wave vector is a priori. Substituting the phase function in the second equation, we inversely get , the constant function.

How many mesh elements do we need to resolve a constant function? Only one! (See this previous blog post on high-frequency modeling.)

The following results show the envelope function and the norm of , ewbe.normE, which is equal to . Here, we can see that we get the correct envelope function if we give the exact phase function, constant one, for any number of meshes, as expected. For confirmation purposes, the phase of , arg(E1z), is also plotted. It is zero, also as expected.

The envelope function (red), the electric field norm (blue), and the phase of the envelope function (green) for the correct phase function k₀x, computed for different mesh sizes.

Now, let’s see what happens if our guess for the phase function is a little bit off — say, instead of the exact . What kind of solutions do we get? Let’s take a look:

The envelope function (red), the electric field norm (blue), and the phase of the envelope function (green) for the wrong phase function, 0.95 k₀x, computed for different mesh sizes.

What we see here for the envelope function is the so-called beating. It’s obvious that everything depends on the mesh size. To understand what’s going on, we need a pencil, paper, and patience.

We knew the answer was , but we had “intentionally” given an incorrect estimate in the COMSOL® software. Substituting the wrong phase function in the second equation, we get . This results in , which is no longer constant one. This is a wave with a wavelength of = 20 um, which is called the beat wavelength.

Let’s take a look at the plot above for six mesh elements. We get exactly what is expected (red line), i.e., . The plot automatically takes the real part, showing . The plots for the lower resolutions still show an approximate solution of the envelope function. This is as expected for finite element simulations: coarser mesh gives more approximate results.

This shows that if we make a wrong guess for the phase function, we get a wrong (beat-convoluted) envelope function. Because of the wrong guess, the envelope function is added a phase of the beating (green line), which is .

What about the norm of ? Look at the blue line in the plots above. It looks like the COMSOL Multiphysics software generated a correct solution for ewbe.normE, which is constant one. Let’s calculate: Substituting both the wrong (analytical) phase function and the wrong (beat-convoluted) envelope function in the second equation, we get , which is the correct fast field!

If we take a norm of , we get a correct solution, constant one. This is what we wanted. Note that we can’t display itself because the domain can be too large, but we can find analytically and display the norm of with a coarse mesh.

This is not a trick. Instead, we see that if the phase function is off, the envelope function will also be off, since it becomes beat-convoluted. However, the norm of the electric field can still be correct. Therefore, it is important that the beat-convoluted envelope function be correctly computed in order to get the correct electric field. The above plots clearly show that. The six-element mesh case gives the completely correct electric field norm because it fully resolves the beat-convoluted envelope function. The other meshes give an approximate solution to the beat-convoluted envelope function depending on the mesh size. They also do so for the field norm. This is a general consequence that holds true for arbitrary cases.

No matter what phase function we use in COMSOL Multiphysics, we are okay as long as we correctly solve the first equation for and as long as the phase function is continuous over the domain. When there are multiple materials in a domain, the continuity of the phase function is also critical to the solution accuracy. We may discuss this in a future blog post, but it is also mentioned in this previous blog post on high-frequency modeling.

2D Example

So far, we have discussed a scalar wave number. More generally, the phase function is specified by the wave vector. When the wave vector is not guessed correctly, it will have vector-valued consequences. Suppose we have the same plane wave from the first example, but we make a wrong guess for the phase, i.e., instead of . In this case, the wave number is correct but the wave vector is off. This time, the beating takes place in 2D.

Let’s start by performing the same calculations as the 1D example. We have and the envelope function is now calculated to be , which is a tilted wave propagating to direction , with the beat wave number and the beat wavelength .

The following plots are the results for θ = 15° for a domain of 3.8637 um x 29.348 um for different max mesh sizes. The same boundary conditions are given as the previous 1D example case. The only difference is that the incident wave on the left boundary is . (Note that we have to give the corresponding wrong boundary condition because our phase guess is wrong.)

In the result for the finest mesh (rightmost), we can confirm that is computed just like we analyzed in the above calculation and the norm of is computed to be constant one. These results are consistent with the 1D example case.

The electric field norm (top) and the envelope function (bottom) for the wrong phase function , computed for different mesh sizes. The color range represents the values from -1 to 1.

Simulating a Lens Using the Beam Envelopes Interface

The ultimate goal here is to simulate an electromagnetic beam through optical lenses in a millimeter-scale domain with the Beam Envelopes interface. How can we achieve this? We already discussed how to compute the right solution. The following example is a simulation for a hard-apertured flat top incident beam on a plano-convex lens with a radius of curvature of 500 um and a refractive index of 1.5 (approximately 1 mm focal length).

Here, we use , which is not accurate at all. In the region before the lens, there is a reflection, which creates an interference. In the lens, there are multiple reflections. After the lens, the phase is spherical so that the beam focuses into a spot. So this phase function is far different from what is happening around the lens. Still, we have a clue. If we plot , we see the beating.

Plot of . The inset shows the finest beat wavelength inside the lens.

As can be seen in the plot, a prominent beating occurs in the lens (see the inset). Actually, the finest beat wavelength is in front of the lens. To prove this, we can perform the same calculations as in the previous examples. The finest beat wavelength is due to the interference between the incident beam and reflected beam, but we can ignore this because it doesn’t contribute to the forward propagation. We can see that the mesh doesn’t resolve the beating before the lens, but let’s ignore this for now.

The beat wavelength in the lens is for the backward beam and for the forward beam for n = 1.5, which we can also prove in the same way as the previous examples. Again, we ignore the backward beam. In the plot, what’s visible is the beating for the forward beam. The backward beam is only a fraction (approximately 4% for n = 1.5 of the incident beam, so it’s not visible). The following figure shows the mesh resolving the beat inside the lens with 10 mesh elements.

The beat wavelength inside the lens. The mesh resolves the beat with 10 mesh elements.

Other than the beating for the propagating beam in the lens, the beating in the subsequent air domain is pretty large, so we can use a coarse mesh here. This may not hold for faster lenses, which have a more rapid quadratic phase and can have a very short beat wavelength. In this example, we must use a finer mesh only in the lens domain to resolve the fastest beating.

The computed field norm is shown at the top of this blog post. To verify the result, we can compute the field at the lens exit surface by using the Frequency Domain interface, and then using the Fresnel diffraction formula to calculate the field at the focus. The result for the field norm agrees very well.

Comparison between the Beam Envelopes interface and Fresnel diffraction formula. The mesh resolves the beat inside the lens with 10 mesh elements.

The following comparison shows the mesh size dependence. We get a pretty good result with our standard recommendation, , which is equal to . This makes it easier to mesh the lens domain.

Mesh size dependence on the field norm at the focus.

As of version 5.3a of the COMSOL® software, the Fresnel Lens tutorial model includes a computation with the Beam Envelopes interface. Fresnel lenses are typically extremely thin (wavelength order). Even if there is diffraction in and around the lens surface discontinuities, the fine mesh around the lens part does not significantly impact the total number of mesh elements.

Concluding Remarks

In this blog post, we discuss what the Beam Envelopes interface does “under the hood” and how we can get accurate solutions for wave optics problems. Even if we get beating, the beat wavelength can be much longer than the wavelength, which makes it possible to simulate large optical systems.

Although it seems tedious to check the mesh size to resolve beating, this is not extra work that is only required for the Beam Envelopes interface. When you use the finite element method, you always need to check the mesh size dependence for accurately computed solutions.

Next Steps

Try it yourself: Download the file for the millimeter-range focal length lens by clicking the button below.

References

1. J. Goodman, Fourier Optics, Roberts and Company Publishers, 2005.

In 1875, John Kerr placed current-carrying coils in holes on either side of a glass slab, which created an electric field. After a polarized beam of light passed through the slab, he noticed that the polarization was different. This difference is related to the change in the glass’ refractive index, which is proportional to the square of the electric field — a phenomenon called the Kerr effect. See how to model this effect and other linear and nonlinear phenomena.

Understanding the Susceptibility of Nonlinear Optical Materials

When an electromagnetic field is applied to a dielectric material, the field displaces the material’s electron from its original orbit, making the electron oscillate at a particular frequency. In other words, the field polarizes the material. The displacement field in this case is represented as a function of the applied electric field as follows:

where E is the applied electric field vector, P is the induced polarization vector, is the vacuum permittivity, and is the isotropic susceptibility.

In the case of an anisotropic dielectric material, the induced polarization vector is a function of the susceptibility tensor as follows:

Finally, in the case of a nonlinear dielectric material, the induced polarization can be expressed as a function of the electric field within the medium through the susceptibility () of the medium and, using a power series expansion, as follows:

where E is the applied electric field, ε₀ is the vacuum permittivity, and is the ith-order susceptibility.

It is assumed that there is no polarization that is independent of E. To have a thorough derivation of the polarization with nonlinear terms, refer to the book by Y. R. Shen (Ref. 5).

First-Order Susceptibility of Optical Materials

First-order susceptibility () deals with the change in refractive index due to the dipole oscillation of the bound and free carriers, such as electrons. Hendrik Lorentz originally came up with the idea of creating a mathematical oscillator model that can relate the dipole oscillation of bound electrons to the susceptibility of the material. Paul Drude originated the idea of oscillation within semiconductors, which deals with free carriers within the material. After combining the effects of bound and free carriers, the new model was called the Drude-Lorentz model.

In the COMSOL Multiphysics® software, the Drude-Lorentz model can be used to define the relative permittivity of a material. To define the Drude-Lorentz model, the relative permittivity at high frequency, plasma frequency, resonance frequency, and damping coefficient need to be given as inputs, as shown below. Multiple oscillators can also be added while assigning each of the oscillators’ contributions.

where ε_r is the complex relative permittivity of the material, ε_∞ is the interband transition contribution to the permittivity, ω_p is the plasma frequency, and Γ is the damping coefficient.

Modeling a Plasmonic Waveguide Filter

To showcase the capability of COMSOL Multiphysics in modeling the Drude-Lorentz material model, a waveguide with a metal-insulator-metal (MIM) interface is modeled. Here, the metal and insulator are modeled as silver and air, respectively. In this configuration, the width of the insulator is made to periodically vary along the waveguide (see the figure below). This particular arrangement of the insulator causes the waveguide to work like a filter known as a plasmonic waveguide filter.

This example shows that the waveguide rejects the electromagnetic radiation of the wavelength between 1.4 um and 1.6 um, but allows the rest of the wavelength (see the figure below). The silver material can be modeled using the Drude-Lorentz approximation, with ε_∞ = 3.7, ω_p = 13.8 rad/s, and Γ = 2.736 rad/s, while the insulator is modeled using air. As an alternative to the Drude-Lorentz material model approximation, the material property determined by Johnson and Christy’s experimental data (Ref. 4), which is available in the Material Library as Ag (Johnson), can be used.

Note that the output characteristic of this plasmonic waveguide filter is similar to that of the fiber Bragg grating (FBG) configuration.

Schematic of the plasmonic waveguide filter. Blue and gray are the insulator and metal domain, respectively. The dashed line depicts a unit cell that is periodically repeated.

The transmittance and reflectance through the plasmonic grating filter (with 10 unit cells) using both the Drude-Lorentz model and Ag (Johnson) from the Material Library. You can download the MPH-file for this model from the Application Gallery.

Second-Order Susceptibility of Optical Materials

There are nonlinear crystals that display relatively high second-order susceptibility (). When a monochromatic beam of light is introduced and passes through such a nonlinear crystal, not only does the output frequency spectrum show the original frequency (ω), but it also indicates the second-order harmonic frequency (2ω). Hence, this phenomenon is called second-harmonic generation (SHG).

The application of SHG lies in the field of laser design and engineering, where it’s challenging to find a material to eject light with shorter wavelengths. For example, when an infrared light source (1064 nm) is pumped through a potassium-dihydrogen-phosphate (KDP) crystal, the crystal ejects a green (532 nm) source of laser light.

In COMSOL Multiphysics, this approach can be modeled either with a transient or frequency-domain analysis in which the polarization is defined using the nonlinear coefficient (d), as shown below. In the transient analysis of the beam, the electric-field-dependent nonlinearity term needs to be introduced to the electric displacement field (D). The way it is introduced in this model is by clever use of the remnant electric displacement (D_r). As a matter of fact, the remnant electric displacement can also accept a nonlinear field quantity, which involves the square of one of the electric field components here. This approach displays the sum frequency generation as well as the difference frequency generation.

where , is the nonlinear coefficient, and E_z is the z-component of the electric field.

With the frequency-domain analysis of the beam, only one particular frequency can be analyzed at one instance. (In other words, only one frequency can be analyzed with the Helmholtz equation.) Hence, the model sets up two interfaces and couples the two physics. The first interface represents the fundamental wave, while the second interface represents the second-harmonic frequency. The polarization of the first interface, , and that of the second interface, , can be defined as the following:

where d is the nonlinear coefficient, is the y-component of the electric field at the fundamental frequency, and is the y-component of the electric field at the second-harmonic frequency.

Left: The output frequency spectrum. The small peak on the left side of the large peak shows the difference frequency generation, while the small peak on the right shows the SHG. Right: The y-components of the electric fields for the fundamental and second-harmonic wave.

Third-Order Susceptibility of Optical Materials

The materials that have dominant third-order susceptibility () display phenomena such as the optical Kerr effect, self-phase modulation, cross-phase modulation, third-harmonic generation, and four-wave mixing. To illustrate the optical Kerr effect in COMSOL Multiphysics, a high-intensity (in the order of GW/cm²) monochromatic beam of light (such as a Nd:YAG laser source) is propagated through a nonlinear crystal made of BK-7. Due to the dominant third-order material nonlinearity in BK-7, the refractive index changes as a function of the beam intensity (I) of the monochromatic input light as follows:

where n₀ is the constant (linear) part of the refractive index, γ is the nonlinear refractive index coefficient, and I is the beam intensity.

The spatially Gaussian-launched beam creates a spatial Gaussian profile of the refractive index, with the peak at the center and decreasing radially outward. This profile of the refractive index causes the beam of light to be more focused at the center during its propagation through the crystal. This phenomenon is called the self-focusing of a laser beam, specifically because the source beam is responsible for its own focusing. This effect is particularly useful in laser engineering, where the self-focusing of a high-power light source in such a narrow central regime can permanently damage the crystal, hence the need to model and compensate for these effects in the design process.

Left: The induced refractive index change, γI, for a high peak intensity, I₀ = 14 GW/cm². Right: The spot radius at the end of the propagation domain versus the peak intensity.

Materials with Electro-Optic Effects

There are materials where the refractive index of the medium can be a function of the applied external electric field, as described in the introduction of this blog post. This applied electric field can be from the DC potential or a slowly varying harmonic potential applied through the coils or contact pads attached to the material. The refractive index optical material property is considered from here on instead of the susceptibility χ.

Mathematically, the refractive index can be represented as a Taylor series expansion of the applied E-field.

For electro-optic materials, the refractive index translates to the following:

where n is the refractive index of the material with no applied E-field, while d₁ and d₂ are the electro-optic coefficients.

About the Pockels Effect

Crystals such as KDP, lithium niobate (LiNbO₃), and cadmium telluride (CdTe) have a refractive index with the dominant first and second terms above. Such media are known as Pockels media, where d₁ is known as the linear optic coefficient because the refractive index is a linear function of the electric field.

In COMSOL Multiphysics, the Pockels effect has been demonstrated using an optical modulator. In this model, light propagates through a single silicon waveguide that branches out into two waveguides. Contact pads are applied to the upper branch and excited with a DC voltage, as shown in the image below. This branch of the waveguide can also be defined as a Pockels medium with d₁ = 30e-12 m/V.

When no voltage is applied to the contact pads, the light flows unimpeded through both the upper and lower branches and interferes constructively at the point where the branches merge together. However, when a certain voltage is applied to the contact pads, a local electric field is created in the region within the contact pads. The material property in the region under the influence of an external electric field modifies the refractive index of this medium, effectively changing the speed of the light propagating through the upper waveguide. When the light propagating in these upper and lower branches interferes at the location where the branches merge, it leads to destructive interference, with no light propagating forward.

The potential application of the Pockels effect lies in designing optical switches; for example, in the field of photonic integrated circuits. In a tutorial model, we demonstrate a particular kind of optical switching element known as a Mach-Zehnder optical modulator.

Schematic of the Mach-Zehnder optical modulator.

Transmission of the upper output branch 1 and lower output branch 2 versus the applied DC voltage.

About the Kerr Effect

There are certain gases, liquids, and crystals that exhibit a centrosymmetric property, where the first and third term of the Taylor expansion are dominant. In such cases, the refractive index can be defined as a quadratic function of the applied E-field as follows:

Concluding Thoughts on Modeling Linear and Nonlinear Optics

Here, we have discussed different optical materials such as KDP, BK-7, LiNbO₃, CdTe, and silicon under an external electric field. These materials show different linear and nonlinear phenomena, such as SHG, self-focusing, and linear and quadratic electric field effects. We have also dealt with the applications of these materials in the laser engineering field, filter design, and optical switches.

Next Steps

Try the tutorials featured in this blog post:

• Plasmonic Waveguide Filter
• Second Harmonic Generation of a Gaussian Beam (Wave Optics)
• Second Harmonic Generation
• Self-Focusing
• Mach-Zehnder Modulator

References

1. J. Leuthold, C. Koos, and W. Freude, “Nonlinear silicon photonics”, NaturePhotonics, vol. 4, pp. 535–544, 2010.
2. Z. Han, E. Forsberg, and S. He, “Surface Plasmon Bragg Gratings Formed in Metal-Insulator-Metal Waveguides,” IEEE Photonics Technology Letters, vol. 19, no. 2, pp. 91–93, Jan. 15, 2007.
3. B. E. A. Saleh and M. C. Teich, Fundamentals of Photonics, John Wiley & Sons, Inc.
4. P. B. Johnson and R. W. Christy, “Optical constants of the noble metals,” Phys. Rev. B, vol. 6, no. 12, pp. 4370–4379, Dec. 15, 1972.
5. Y. R. Shen, The Principles of Nonlinear Optics, John Wiley & Sons, Inc.

During his life, John Scott Russell chased his passion for science — literally. While watching horses pull a boat through a shallow canal, he noticed a wave behaving strangely and followed it for one or two miles on horseback. For the rest of his life, he continued to chase this wave (which he called the “wave of translation”) figuratively, persevering even when his theories were ridiculed by scientists. Did Scott Russell ever catch up to his wave?

A Horse, a Flyboat, and a Curious Naval Architect

If you lived in Glasgow in the 1830s, one of the best ways to get around Scotland was a horse-drawn flyboat on the Glasgow, Paisley and Ardrossan Canal. Flyboats were lightweight, long, and narrow. They were pulled through the shallow water of the canal by horses.

A modern view of Glasgow, Scotland, (left) and a canal in central Scotland, home of the rotating boat lift known as the Falkirk Wheel (right).

One day, William Houston, an owner of one of the flyboat companies, was traveling down a canal when the horse pulling his flyboat was startled and bolted. Houston noticed something strange: The water exhibited no resistance. The ship glided fast (similar to what we now call “hydroplaning”), and the turbulence from the boat’s movement didn’t damage the shores of the canal. (Ref. 1)

Enter John Scott Russell, a naval architect from Glasgow. When he heard about the phenomenon Houston observed, he thought that witnessing it for himself could give him insight into boat design. While observing the canal, one of the horses suddenly stopped. A wave formed under the middle of the boat, moved to the prow, and then took off past the boat entirely. Scott Russell followed the wave, first on foot and then on his horse. He was astounded to see that the wave kept going at the same size and pace. He later called it “the wave of translation” and described the event as “the happiest day of my life.” (Ref. 2)

John Scott Russell in 1847. Image in the public domain in the United States, via Wikimedia Commons.

Scott Russell devoted two years to replicating the wave of translation so he could study it further. He even built a 30-foot basin to test his different theories. Eventually, he observed some unique properties of these waves, which he now called solitary waves. According to Scott Russell, a solitary wave:

• Travels over large distances in a stable manner
• Travels at a speed that is dependent on its size
• Has a width that is dependent on the water’s depth
• Does not combine with other waves (instead, large ones overtake smaller ones)
• Splits into two waves of different sizes if it is too large for the depth of the water

Animation showing the behavior of a solitary wave.

He also categorized these waves into four types:

1. Waves of translation, which involve mass transfer and are either solitary or followed by a series of secondary waves
2. Oscillatory waves, groups of successive waves (such as the waves created by wind)
3. Capillary waves, which are caused by a very small agitation of the water and depend on surface tension
4. Corpuscular waves, rapid successions of solitary waves (such as sound waves)

Scott Russell presented his findings at a British Science Association meeting in Edinburgh, describing the waves and the mechanics behind them. His work contained a few misinterpretations of the foundations of mechanical laws — understandably so, as his background was in architecture, not physics. Scientists at the time balked at his theories and distrusted his lack of engineering and physics expertise.

And so began a lifetime — actually, many lifetimes — of investigating the behavior of solitary waves.

Initial Reactions to the Solitary Wave

At first, Scott Russell didn’t earn many fans in the scientific community regarding his theory of solitary waves. George Biddell Airy, who studied the behavior of waves in relation to the tides, did not hold Scott Russell in high regard and believed that solitary waves contradicted Pierre-Simon Laplace’s theory of fluid mechanics. Laplace’s equations, as we know, are integral to the study of fluid dynamics today. (Ref. 1)

George Gabriel Stokes, of the famed Navier-Stokes equations, also did not support the possibility of solitary waves and initially condemned their relation to tides and sound. Over time, as he researched finite oscillatory waves, he changed his stance and admitted that a theoretical solitary wave was plausible. (Ref. 1)

Meanwhile: A Return to Shipbuilding

Scott Russell never gave up the subject of solitary waves, but he continued what his main job description entailed: building ships. He used his research into waves to design a special ship prow, which was based on the shape of a versed sine wave, that could better handle water resistance.

In the 1850s, Isambard Kingdom Brunel asked for Scott Russell’s help regarding a steamship called the Great Eastern. Brunel had designed the ship, which was slated to be the largest ship of its time (he affectionately called it his “Great Babe”). The ship could purportedly travel from England to Australia without needing to refuel.

The Great Eastern before its first launch. Image in the public domain in the United States, via Wikimedia Commons.

Scott Russell was successful in taking Brunel’s designs and building the Great Eastern, which eventually made many transatlantic voyages. However, his success was tarnished when Brunel passed away shortly before launch and a major accident occurred during the ship’s maiden voyage. Around this time, Scott Russell was also having trouble with his finances and was dealing with the seizure of his assets.

How the Tides Turned: Boussinesq and the KdV Equation

Toward the end of his life, Scott Russell’s solitary wave was still rebuked by scientists, and he was bankrupt. Fortunately, things were about to change.

Joseph Valentin Boussinesq, a protégé of Adhémar Jean Claude Barré de Saint-Venant known for his contributions to the field of fluid dynamics, did not write off Scott Russell like others at the time. Instead, he subjected every aspect of waves and tides to mathematical analysis. In 1872, Boussinesq attempted to explain shallow water waves, which led to an equation that proved solitary waves are theoretically possible. He even mentioned Scott Russell in his paper on the subject in 1877. Lord Rayleigh independently developed similar theories on waves and also supported Scott Russell. (Ref. 1)

Finally, two scientists had spoken out in support of his work! Then, in 1882, Scott Russell passed away at the age of 74 on the Isle of Wight, England. But the story doesn’t end there.

In 1895, Diederik Korteweg and Gustav de Vries expanded on Boussinesq’s work and developed an equation that proves solitary waves are theoretically possible. The KdV equation doesn’t introduce dissipation, which means it can be used to describe waves that travel long distances while retaining their shape and speed. The equation is also simpler than Boussinesq’s version and gives a better solution. (Ref. 2) Because of these advantages, the KdV equation is still used to understand wave behavior — in its many forms — today.

Modern Research into Solitons

Research into solitary waves picked up in 1965, when researchers Martin Krustal and Norman Zabusky studied the KdV equation in more detail. They found that solitary waves can occur not just theoretically but also naturally, coining the term solitons to describe them. In addition, solitons were not just thought of in the context of water waves anymore — with research into applications for optics, acoustics, and other areas.

Krustal, along with researchers Gardner, Greene, and Miura, developed the inverse scattering transform in 1967. This method can be used to find the exact solution of the KdV equation and also demonstrates the elastic collisions between waves, originally observed by Krustal and Zabusky. (Ref. 2)

A hydrodynamic soliton. Image by Christophe.Finot et Kamal HAMMANI. Licensed under CC BY-SA 2.5, via Wikimedia Commons.

Moving forward, scientists Zakharov and Shabat used a formulation developed by Peter Lax to solve the nonlinear Schrödinger equation, which describes the evolution of the slowly varying envelope of a general wave packet. Ablowitz, Kaup, Newell, and Segur later came up with a more systematic approach to solving the nonlinear Schrödinger equation, which is now known as the AKNS method. (Ref. 2)

All of this mathematical activity around solitons caught the attention of the scientific community in a way that Scott Russell couldn’t. Over the next 30 years, solitons in a wide range of different fields were researched, including geomechanics, oceanography, astrophysics, quantum mechanics, and more.

Solitons for Fiber Optics

Optical fibers are an important and practical application area for solitons. The linear dispersion properties of a fiber level out a soliton, while its nonlinear properties help the soliton achieve a focusing effect. The result is a very stable pulse that can travel for what seems like forever.

The behavior was first observed by a group at Bell Labs led by Linn Mollenauer in the 1980s that aimed to apply solitons to long-distance telecommunication systems. In the 1990s, a team of MIT researchers added optical filters to a transmission system in an attempt to maximize an optical soliton’s propagation distance. Using this method, Mollenauer’s group sent a 10-Gbit/s signal more than 20,000 km — impressive for the time. (Ref. 2) During the 2000s, optical soliton research ventured into the field of vector solitons, which have two distinct polarization components.

Current research from Lahav et al. aims to create solitons that are stable in all three dimensions, known as “light bullets”. This requires the simultaneous cancellation of diffraction and dispersion, which has been achieved with a highly structured material, but not with an unstructured one that can be used in practical applications. The Lahav group has investigated the fundamental properties of 3D solitons to develop more technological applications of solitons for fiber optics. They have also developed a method that involves shining a repetitive string of light pulses into a special material called “strontium barium niobate” to create a self-guided beam and cancel out the dispersion. This method creates a string of 3D solitons that could potentially be used in advanced nonlinear optics and optical information processing. (Ref. 3)

Equation-Based Modeling Enables Out-of-the-Box Soliton Analysis

The solution to the KdV equation tells us that the speed of a soliton determines its amplitude and width. By investigating this effect, we can better predict the behavior and limitations of solitons for optical applications. Simulation can be used to visualize soliton behavior beyond numerical equations, without setting up resource-intensive or costly optical experiments. Besides demonstrating how speed influences the amplitude and width of a wave, simulation also shows how solitons collide and reappear while maintaining their shape (like the solitary waves Scott Russell observed “overtaking” each other in the ocean).

Simulation results that show solitons colliding and reappearing. Image from The KdV Equation and Solitons tutorial model.

Predefined physics settings are an efficient and easy option for straightforward modeling tasks; however, optical solitons are anything but. Equation-based modeling enables you to expand what is normally possible with simulation for problems that require flexibility and creativity. Using equation-based modeling, you can seamlessly implement the KdV equation into the COMSOL Multiphysics® software by adding partial differential equations (PDEs) and ordinary differential equations (ODEs). You can even create a physics interface from your custom settings so that you don’t have to start from scratch the next time you need to set up a model.

Adding a PDE to a soliton model in the COMSOL Multiphysics graphical user interface (GUI), an example of equation-based modeling.

Equation-based modeling functionality makes it possible to simulate an initial pulse in an optical fiber as well as the resulting waves or solitons.

Concluding Thoughts on John Scott Russell, the Individual Wave

In 1885, Scott Russell’s book The Wave of Translation in the Oceans of Water, Air and Ether was published posthumously. It included his speculations on the physics of matter and how we can find the depths of the atmosphere and universe by computing the velocity of sound and light, respectively. (Ref. 4) Even at the end of his life, Scott Russell continued to theorize on how we can apply mathematics to the observable world as well as the significance of solitons in modern physics. If only he could have seen the development of the KdV equation or recent advancements in optics.

One of Scott Russell’s supporters, Osborne Reynolds, made a fitting observation in his own research of solitary waves: In deep water, groups of waves travel faster than the individual waves from which they were made. (Ref. 1) Perhaps we can think of John Scott Russell as the individual wave, inspiring others to keep moving toward a common goal.

Next Step

Learn more about equation-based modeling, and the other features and functionality in COMSOL Multiphysics, by clicking the button below.

References

1. O. Darrigol, “The Spirited Horse, the Engineer, and the Mathematician: Water Waves in Nineteenth-Century Hydrodynamics,” Archive for History of Exact Sciences, vol. 58, pp. 21–95, 2003.
2. B. Kath and B. Kath, “Making Waves: Solitons and Their Optical Applications,” SIAM News, vol. 31, no. 2, pp. 1–5, 1998.
3. F.W. Wise, “Solitons divide and conquer,” Nature, vol. 554, pp. 179–180, 2018.
4. Topics in Current Physics: Solitons, R.K. Bullough and P.J. Caudrey, eds., Springer-Verlag, pp. 373–379, 1980.

In a previous blog post, we discussed the paraxial Gaussian beam formula. Today, we’ll talk about a more accurate formulation for Gaussian beams, available as of version 5.3a of the COMSOL® software. This formulation based on a plane wave expansion can handle nonparaxial Gaussian beams more accurately than the conventional paraxial formulation.

Paraxiality of Gaussian Beams

The well-known Gaussian beam formula is only valid for paraxial Gaussian beams. Paraxial means that the beam mainly propagates along the optical axis. There are several papers that talk about paraxiality in a quantitative sense (see Ref. 1).

Roughly speaking, if the beam waist size is near the wavelength, the beam propagates at a higher angle to a focus. Therefore, the paraxiality assumption breaks down and the formulation is no longer accurate. To alleviate this problem and to provide you with a more general and accurate formulation for general Gaussian beams, we introduced a nonpariaxial Gaussian beam formulation. In the user interface this is referred to as Plane wave expansion.

The method is based on the angular spectrum of plane waves (Ref. 2) and is sometimes referred to as the angular spectrum method (Ref. 3).

Angular Spectrum of Plane Waves

Let’s briefly review the paraxial Gaussian beam formula in 2D (for the sake of better visuals and understanding).

We start from Maxwell’s equations assuming time-harmonic fields, from which we get the following Helmholtz’s equation for the out-of-plane electric field with the wavelength for our choice of polarization:

where .

The angular spectrum of plane waves is based on the following simple fact: an arbitrary field that satisfies the above Helmholtz equation can be expressed as the following plane wave expansion:

where is an arbitrary function.

The integration path is a circle of radius for real and . (For complex and , the integration domain extends to a complex plane.) The function is called the angular spectrum function. One can prove that this satisfies Helmholtz’s equation by direct substitution.

Now that we know that this formulation always gives exact solutions to Helmholtz’s equation, let’s try to understand it visually. From the constraint, , we can set and and rewrite the above equation as:

The meaning of the above formula is that it constructs a wave as a sum, or integral, consisting of many waves propagating in various directions, all with the same wave number . This is shown in the following figure.

Visualization of the angular spectrum of plane waves.

When actually solving a problem using this formula, all you have to do is find the angular spectrum function that satisfies the boundary conditions. By assuming that the profile of the transverse field (perpendicular to the propagating direction, i.e., optical axis) is also a Gaussian shape (see Ref. 4), one can derive that , where is the spectrum width.

By some more mathematical manipulations, we get a relationship between the spectrum width and the beam waist radius . For example, for a slow Gaussian beam, the angular spectrum is narrow. A plane wave, on the other hand, is the extreme case where the angular spectrum function is a delta function. For a fast Gaussian beam, the angular spectrum is wider, and vice versa.

This was a quick summary of the underlying theory for nonparaxial Gaussian beams. To recap what we have shown so far, let’s rewrite the formula once more by using polar coordinates, :

This is the formulation that Born and Wolf (Ref. 2) use in their book.

The 3D formula is more complicated and looks different due to polarization, but the basic idea is the same as seen in the references mentioned above. It can also look different depending on whether or not you consider evanescent waves. The Plane Wave Expansion method used in the Wave Optics Module and the RF Module, although based on the angular spectrum theory, is adapted for numerical computations.

Plane Wave Expansion: Settings and Results

Let’s compare the new feature, Plane wave expansion, with the previously available feature, Paraxial approximation. The Settings window covering both methods is shown below.

The Plane Wave Expansion feature settings.

With the new feature, you have two options if the Automatic setting doesn’t give you a satisfactory approximation:

1. Wave vector count
2. Maximum transverse wave number

The first option determines the number of discretization levels, depending on how fine you want to represent the Gaussian beam. The more plane waves, the finer it gets. The second option is related to the integral bound in the previous equation; i.e., . This integral bound can be the maximum for the smallest possible spot size and can be more shallow for slower beams, depending on how fast the Gaussian beam is. You need more angled plane waves with a larger transverse wave number to represent faster (more focused) beams.

The following results compare the two formulas for the case where the spot radius is , which is considerably nonparaxial. As in the previous blog post, the simulation is done with the Scattered Field formulation and the domain is surrounded by a perfectly matched layer (PML). This way, the scattered field represents the error from the exact Helmholtz solution.

The left images below show the new feature, while the images on the right show the paraxial approximation. The top images show the norm of the computed Gaussian beam background field, ewfd.Ebz, while the bottom images show the scattered field norm, ewfd.relEz, which represents the error from the exact Helmholtz solution. Obviously, the error from the Helmholtz solution is greatly reduced in the nonparaxial method.

Comparison between the angular spectrum of plane waves and the paraxial formula.

Concluding Remarks

We have discussed the theory and results for an approximation method for nonparaxial Gaussian beams using the new plane wave expansion option. Remember that this formulation is extremely accurate, but is still an approximation under assumptions. First, we have made an assumption for the field shape in the focal plane. Second, we assume that the evanescent field is zero. If you are interested in the field coupling to some nanostructure near the focal region in a fast Gaussian beam, you may need to calculate the evanescent field.

Next Step

Learn more about the formulations and features available for modeling optically large problems in the COMSOL® software by clicking the button below:

Note: This functionality can also be found in the RF Module.

References

1. P. Vaveliuk, “Limits of the paraxial approximation in laser beams”, Optics Letters, vol. 32, no. 8, 2007.
2. M. Born and E. Wolf, Principles of Optics, ed. 7, Cambridge University Press, 1999.
3. J. W. Goodman, Fourier Optics.
4. G. P. Agrawal and M. Lax, “Free-space wave propagation beyond the paraxial approximation”, Phys. Rev. a. 27, pp. 1693–1695, 1983.

If you ever visit the extravagant dome within St. Paul’s Cathedral in London, be careful what you say. As Lord Rayleigh discovered circa 1878, the vaulted structure exhibits an interesting acoustics phenomenon: Whispers from one part of the dome can be clearly heard in other areas. Rayleigh called the effect a “whispering gallery”. Surprisingly, you can observe a similar effect in another field of science entirely: light waves traveling in an optical ring resonator.

What Is an Optical Ring Resonator?

Like optical filters, optical ring resonators are waveguide structures that allow only a narrow band of frequency. They can also be used to couple two optical waveguides in opposite directions. A typical optical ring resonator has two parts:

1. A straight waveguide
2. A ring waveguide

The waveguide cores are placed close together and light waves are coupled from one waveguide to the other.

An optical ring resonator (left) exhibits an effect similar to that of a whispering gallery (right), but with light waves instead of sound. Right: The whispering gallery at St. Paul’s Cathedral in London. Image by Femtoquake — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.

In the field of silicon photonics, optical ring resonators show potential as components for photonic integrated circuits. Due to the resonators’ high refractive index contrast, extremely small circuits can be produced. In addition, two or more optical ring resonators can be combined to develop high-order optical filters with compact size, minimal losses, and easy integration into existing networks. Other applications of optical ring resonators include tunable mechanical sensors, biosensors and spectroscopy, as well as quantum photon research.

In an optical ring resonator, light propagates around the loop and remains in the waveguides because of total internal reflection (TIR), a phenomenon in which light rays do not refract through the boundary of the medium they strike.

Light propagation in an optical ring resonator.

Since only a few wavelengths reach resonance within these loops, optical ring resonators are used as filters. The transmission loss of the resonator’s coupler balances the loss for the propagating wave, which is ideal for notch filters especially.

Simulating an Optical Ring Resonator in the COMSOL® Software

Wave optics modeling software is helpful for evaluating the spectral properties of optical ring resonators. For example, you can use the COMSOL Multiphysics® software and the add-on Wave Optics Module, which includes the predefined Electromagnetic Waves, Beam Envelopes interface. This interface is used to model optical wave propagation over many wavelengths and the results can help you evaluate the performance of an optical ring resonator as a notch filter.

The Electromagnetic Waves, Beam Envelopes interface is based on the beam envelope method, a numerical method used to analyze the slowly varying electric field envelope for an optically large simulation. When compared to traditional optical analysis methods, the beam envelope method doesn’t require a fine mesh to resolve the propagating waves. This makes it a computationally efficient option.

An optical ring resonator with a phase jump at the boundary between both waveguides (y = 0).

At the boundary between the straight and ring waveguides, there is a discontinuous phase approximation. By implementing a Field Continuity boundary condition, you can handle this phase discontinuity as well as that of the field envelope. The boundary condition makes it so the electric and magnetic fields have continuous tangential components at the boundary, even with a phase jump.

Evaluating the Simulation Results

To calculate the spectral properties of the model, boundary-mode analyses and a frequency-domain study are run using the specialized modeling features for wave optics. Below, you can see a field plot of the resonant wavelength. These results show that when the field in the straight waveguide interferes with the field from the ring waveguide, they are out of phase; therefore, the outgoing field in the straight waveguide is almost zero. Since nearly no light is being transmitted from the straight waveguide, this optical ring resonator can be considered a well-designed notch filter.

You could test the parameters of the model to design an improved optical ring resonator that completely blocks light at the resonant wavelength — perhaps even by building an app to efficiently run multiple analyses.

Next Steps

Check out these related resources:

• Blog post on simulating silicon photonics applications
• Quick video demonstrating the beam envelope method for wave optics modeling

When it comes to synchrotron light sources, brighter is better. By using bright beams in their accelerator, researchers at the Advanced Proton Source (APS) synchrotron facility can efficiently gather detailed data. In collaboration with APS engineers, Nicholas Goldring of RadiaSoft LLC creates and distributes simulation applications for designing vacuum chambers relevant to the APS. Below, find a video recording and summary of his keynote talk from the COMSOL Conference 2018 Boston.

Nicholas Goldring Discusses Simulation Applications for Synchrotron Design

Optimizing Electron Beam Brightness at the APS Synchrotron Facility

RadiaSoft LLC models and designs particle accelerators and X-ray beamlines and is currently working with Argonne National Laboratory to improve vacuum chamber simulations. The goal of the APS upgrade is to improve the brightness of the X-ray beams, which, according to Goldring, is “a figure of merit for synchrotron light sources.” Increasing the beam intensity requires the bending magnet pole tips to be closer to the electron beam axis, which in turn requires smaller vacuum chambers. To fit the new design, the chambers must be scaled down from 190 mm to 22 mm, making the synchrotron’s behavior even more complex. As Goldring said: “Not only do we have a much brighter beam and higher-intensity X-rays, the vacuum chambers need to be smaller, resulting in complex and coupled physical phenomena, including high thermal stresses, photon stimulated desorption, and electromagnetic wakefields.”

From the video: Nicholas Goldring discusses the beam brightness (top right) and vacuum chambers (bottom right) before and after the upgrade.

To accurately simulate the behavior of the APS synchrotron and other accelerators, RadiaSoft creates models, turns them into simulation applications, and then distributes them to project stakeholders.

Upgrading Accelerator Designs with Simulation Applications and COMSOL Server

The synchrotron vacuum chamber is a true multiphysics problem, but in a typical accelerator simulation, Goldring explained that “there are many different codes […] and they are very specialized” — usually to one physical process. This is problematic because going back and forth between simulations is error prone and time consuming.

As a solution to this issue, the engineers at RadiaSoft use the COMSOL Multiphysics® software for ray tracing, thermal analysis, molecular flow models, and more. After building a model, they turn it into a simulation application and distribute it using the COMSOL Server deployment product. This enables scientists and engineers who aren’t familiar with the codes or COMSOL Multiphysics to run their own simulations.

Goldring said that the Application Builder’s interface makes things simple, enabling him to “drag-and-drop lots of different model objects onto a canvas.” In addition, more sophistication can be added to an application via the built-in Java® development environment, such as by implementing custom algorithms. Further, Goldring said: “COMSOL® has an extensive [application program interface], but they make it easy to access by recording methods.” Colleagues can easily access the applications on Radiasoft’s cloud-based servers via COMSOL Server, which Goldring said “works out very nicely.”

Example: Rays in a Vacuum Chamber

The first application that Goldring discussed is for the rays in the new vacuum chamber design. App users can define a number of parameters, including the:

• Electron beam source
• Arc length of the beam
• Bending radius
• Energy of beam
• Strength of dipole magnets

Based on these (and other) inputs, the application shows the temperature in the chamber as well as the energy and power distribution of the rays. Goldring said: “Synchrotron radiation power distribution is fairly complicated, especially as it progresses along the electron trajectory, so it’s often nice to plot what that distribution is like at various points.”

From the video: Nicholas Goldring showing the vacuum chamber application.

By deploying their simulation applications with COMSOL Server, RadiaSoft is making it easier for scientists and engineers to test and optimize accelerator designs.

This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC0015209.

To learn more about how RadiaSoft uses multiphysics modeling and applications to improve the APS synchrotron, watch the keynote video at the top of this post and visit the RadiaSoft website.

In 1980, Eli Yablonovitch from Bell Communication Research pondered how to reduce losses in semiconductor lasers in a specific frequency range. He sliced periodic circular holes in a transparent medium and observed that it didn’t allow the frequency range causing the losses to pass through. Yablonovitch found that these structures work similarly to semiconductors with conduction and valence bands and named them photonic crystals (with Sajeev John from Princeton University). Let’s discuss three examples in which photonic crystals control light.

Bending Light with a Photonic Crystal

When GaAs pillars are arranged in a periodic manner, as shown in the figure below, the device has the ability to bend light with an angle (90° in this case) and also act as a filter for a band of frequencies (also called a photonic band gap).

Schematic of a photonic crystal.

To model this photonic crystal in the COMSOL Multiphysics® software and add-on Wave Optics Module, the transverse electric (TE) wave (polarized in the z direction) is made to propagate through the left boundary using the Scattering boundary condition and an amplitude of 1 V/m. The rest of the boundaries are assigned Scattering boundary conditions with no incident fields. When we run the model with a sweep of different wavelengths for the incident light source, we get a graph of the transmittance and reflections, as shown below.

Normalized transmittance of the photonic crystal.

Left: Passband at a 1000-nm wavelength. Right: Stopband at a 700-nm wavelength.

Modeling a Photonic Crystal Fiber

A step-index fiber guides light through the high refractive index of the core, while a photonic crystal fiber (PCF) is made up of microstructured optical fibers that guide light either through index guiding or band gap confinement. In this blog post, we focus on index-guided PCF, where the core of the PCF is made of cladding material and is surrounded by air-filled holes. We assume the air hole’s radius as 0.3*pitch, where the pitch is the distance between adjacent holes.

Schematic of index-guided photonic crystal.

To plot the dispersion diagram (the effective refractive index vs. the normalized wavelength), we perform a mode analysis along with a parametric sweep over the hole radius from 0.23 um to 4.69 um. To detect the fundamental and higher-order modes, the number of modes to search is increased to 50. The challenge then becomes correctly identifying the fundamental and higher-order modes from a total of 50 identified modes. One approach to identify these modes is to perform an integration in the core region for different effective mode indices (or effective refractive indices).

Power integrated in the core region vs. the effective mode index number for a 4.65-um hole radius and 15.5-um pitch.

There are two approaches to filter out unnecessary modes and capture only the meaningful fundamental and higher-order modes:

1. Apply a filter to the power; for example, the required effective refractive index is then ewfd.neff*(intop1(ewfd.Poavz)>P_threshold), where P_threshold is the power that will eliminate the unnecessary modes
2. Observe the effective mode index number for the fundamental and higher-order modes and if it is getting repeated

In this case, we observe that the fundamental mode is repeated between effective mode index numbers 40 and 45, and higher-order modes were repeated between effective mode index numbers 20 and 25. The dispersion diagram is plotted by included both of these filters to remove the unnecessary modes. The dispersion diagram matches well with Figure 4, Chapter 9 in Ref. 1.

Dispersion diagram: effective refractive index vs. normalized wavelength (lda0/pitch).

Analyzing a Photonic Band Gap

An alternate approach to modeling the band gap is to formulate an eigenvalue problem, as shown in the Band Gap Analysis of a Photonic Crystal model. In this case, a periodic arrangement of GaAs pillars is modeled in which the pillars are placed equidistant from each other. Instead of modeling an array of GaAs pillars, as we did in the first example, we model only a single unit cell and apply a Floquet periodic boundary condition, as shown below.

Array to unit approximation with the Periodic boundary condition applied at +/- X and +/-Y.

An auxiliary sweep is performed on the wave vector k from 0 to 0.5 to evaluate the dispersion relation in the (1,1) direction. Additionally, the refractive index of the GaAs material is considered frequency dependent. As can be seen below from the dispersion relationship, there is no EM wave propagation surviving in the (1,1) direction between bands 3 and 4, also known as the band gap of the photonic crystal.

Dispersion relation when the wave vector is varied from 0 to 0.5 in the (1,1) direction.

Final Thoughts on Photonic Crystals

There are different approaches to modeling photonic crystal devices, whether you perform a parametric sweep of different frequencies, analyze the modes, or solve for the eigenvalues. Photonic crystals can work as filters and tools to engineer the path of light, which is especially helpful while designing photonic integrated circuits. Additionally, when performing mode analysis, integrating the power at the core region and filtering the certain mode index number can help to delineate the fundamental and higher-order modes from other unnecessary modes. Finally, a unit cell model, along with Floquet periodic boundary conditions, can be modeled to perform band gap analysis.

Next Steps

Learn more about the specialized functionality for modeling photonic crystals in the COMSOL® software:

• Try the tutorial models featured in this blog post:
  • Photonic Crystal
  • Photonic Crystal Fiber Blog Model
  • Band-Gap Analysis of a Photonic Crystal
• Learn more about silicon photonics on the COMSOL Blog:
  • Silicon Photonics: Designing and Prototyping Silicon Waveguides
  • How to Model Optical Anisotropic Media with COMSOL Multiphysics®

Reference

1. J.D. Joannopoulus, R.D. Meade, and J.N. Winn, Photonic Crystals (Modeling the Flow of Light), Princeton University Press, 2008.

The curl element, sometimes called edge element or vector element, is widely used in the finite element method to solve electromagnetics problems. This blog post gives a comprehensive introduction to this type of element, including why and how it is used in the COMSOL Multiphysics® software. The understanding of why and how the curl element is used, however, is not straightforward. Therefore, we will first review some background information about Maxwell’s equations and the finite element method.

2 Basic Forms of Equations to Be Solved in Electromagnetics

The aim of electromagnetics modeling is to solve Maxwell’s equations subject to certain boundary conditions. Maxwell’s equations in their differential form are given as:

(1)

(2)

(3)

(4)

where  and  are the electric and magnetic field intensity, respectively;  and  are the electric and magnetic flux density, respectively; and  and  are the electric charge density and electric conduction current density, respectively.

To obtain a closed system, Maxwell’s equation include constitutive relations that describe the macroscopic properties of the medium. With COMSOL Multiphysics, you can model a wide range of different medium, including nonnlinear and anisotropic materials. However, for the sake of simplicity, we neglect the remanent effect and assume the medium is linear and isotropic, resulting in a simple constitutive relation given as:

(5)

where  is the permittivity and  is the permeability of the medium. 

Note that equations (1) – (4) are valid at points in a continuous medium, while at the discontinuous interface between medium 1 and 2, we have the boundary conditions expressed as:

(6)

(7)

(8)

(9)

where  is the outward normal from medium 2 and  and  the surface electric charge density and surface current density, respectively.

Equations (7) and (8) imply that the tangential electric field and normal component of the magnetic flux field are continuous at the boundary, while Eq. (6) and (9) imply that the normal component of the electric flux field and the tangential magnetic field can be discontinuous.

For specific problems, it is always convenient to solve subsets or special cases of Maxwell’s equations, resulting in different electric, magnetic, or electromagnetic formulations. Based on these formulations, COMSOL Multiphysics has several electromagnetics modules (for instance, the AC/DC Module, RF Module, and Wave Optics Module), as well as several different physics interfaces for each module.

For example, the Electrostatics interface in the AC/DC Module models electrostatics problems where only the static charge is present. In this situation, we only need to solve equations (1) and (2). By introducing the electric potential  and defining , equations (1) and (2) are reduced to a single equation, Poisson’s equation, since  always holds. Poisson’s equation is expressed as:

(10)

In COMSOL Multiphysics, all of the electric scalar potential interfaces are formulated as a version of Poisson’s equation. For a magnetic field without a current, equation (4) is reduced to a form similar to that of a static electric field. By introducing a magnetic scalar potential, the problem can also be formulated into Poisson’s equation. For other cases, we have to deal with the vector formulation. For example, in a magnetostatics situation where only a static current is present, we only need to solve equations (3) and (4). By introducing the magnetic vector potential  and defining , equations (3) and (4) are reduced to one equation below, since  always holds.

(11)

Equation (11) is written in the form of vector equation that contains the  operator. In fact, other situations, such as electromagnetic waves are also formulated in this form. 

To facilitate discussion, we take the time-harmonic electric field as an example. In the frequency domain, inserting equation (2) into equation (4) yields

(12)

where  is the frequency and  is the imaginary unit.

Shape Functions and Lagrange Elements

In COMSOL Multiphysics, the finite element method (FEM) is generally used to solve partial differential equations (PDEs), and Maxwell’s equations are no exception. The finite element method is used to solve PDEs in several steps, including:

1. Divide the domain into many small, nonoverlapping elements, which are called mesh elements.
2. The solution is in each element approximated by a local shape function or basis function.
3. Write the PDEs in weak forms, discretize on each mesh element to obtain local matrices.
4. Assemble local matrices to a global matrix, and solve it.

Let us take Poisson’s equation (10) as an example to show how FEM works. We can use different elements depending on the shape function used. For the sake of simplicity, we consider the domain is in 2D and use a linear triangular Lagrange element. The electric potential  in an element with vertices can be approximated with the linear function as

(13)

from which we can see that each vertex adds a degree of freedom (DOF), and the corresponding shape function equals one at the vertex but zero at all other vertices. The higher-order Lagrange element adds DOFs not only on vertices but also on other nodes that lie in the element. Thus the Lagrange element is also called the nodal element. The shape functions of a linear triangular Lagrange element are visualized below.

The Lagrange elements are not only continuous in each element but also continuous across boundaries, as shown in the figure below.

Medium 1 and medium 2 share the same boundary, . The electric field close to the boundary is plotted in blue and red arrows in mediums 1 and 2, respectively. Since the electric potential  is continuous across boundaries, the tangential gradient of  (i.e., the tangential electric field) is continuous. In order words, the boundary condition Eq. (7) is automatically satisfied. Thus, we only need to consider Eq. (6) where surface charges are present. Next, we will show how this could be naturally handled by the FEM.

The derivation of the weak form for Poisson’s equation (10) is not difficult. Multiply the test function  to both sides of equation (10) , and the integral over the domain  gives

(14)

Applying the integration by parts for the left-hand side yields

(15)

with  being the boundary of the domain and  the normal vector oriented away from the domain.

This step is of great importance and has two main advantages:

1. Reducing the maximum order of spatial derivatives, which makes it possible to solve the second-order PDE with linear (first-order) elements
2. Making it clear what the natural boundary condition (automatically satisfied if not consider it) is for the equation

The second integral on the left-hand side disappears if the normal component of  vanishes on the boundary. To clearly see how it works, it is convenient to rewrite equation (15) as

(16)

where it is clear that the natural boundary condition is .

In the Electrostatics interface of the AC/DC Module, this natural boundary condition is set as the default. For situations where the boundary condition is not given by the electric potential but by the electric charge density, it is straightforward to incorporate the boundary condition Eq. (6) to equation (16).

Curl Elements

It is also possible to use Lagrange-element-based FEM to solve the vector equation (12) by dividing it into different components, . However, it is complicated to implement the boundary conditions, especially for irregular boundaries. Even so, the results could be spurious, since the Lagrange element would enforce each component  to be continuous across the boundary, which violates the fact that the normal component of electric field can be discontinuous at material interfaces, especially at boundaries from sharp corners.

Let’s take the Sierpinski Fractal Monopole Antenna model from the Application Library as an example. The surface electric field of the fractal radiator at 1.6 GHz is shown below. It is clear that  greatly changes across the edges. 

As shown earlier, the Lagrange element uses scalar shape functions to approximate the scalar field. It is natural to use vector shape functions to approximate the vector field. For instance, the electric field in equation (12) can be expressed as:

(17)

As equation (17) indicates, it is not suitable to add DOFs on nodes, since a vector field also has a direction. To obtain a scalar value, we could add DOFs on each edge, since the vector field component along the edge (tangential component) is a scalar. Then, we rewrite equation (17) as:

(18)

Similar to the Lagrange shape function, the tangential component of the vector shape function along one edge is a non-zero constant, and along the other edges, equal to zero. One type of shape function that satisfies the above property is the Whitney 1-form basis function (Ref. 1, Ref. 2), which is expressed as:

(19)

The shape functions of the first-order triangular edge element are plotted below.

From the mathematics point of view, the edge element is conforming in the  space (Ref. 3), thus it is also called a curl element. In COMSOL Multiphysics, we use the more general name ‘curl element’ since the higher-order elements add more DOFs not only on the edges, but also inside the element. Similar to what we have plotted for two adjacent Lagrange elements, the basis functions of two curl elements sharing the same boundary  are shown below

We can see that the tangential electric field across the boundary is continuous, which is very similar to the case of using Lagrange elements to solve Poisson equation. Therefore, by using the curl elements, the boundary condition Eq. (7) is automatically fulfilled. Let us then show how boundary Eq. (9) is handled by FEM.

Similar to solving Poisson’s equation, multiply the test function  to both sides of equation (12), and the integral over the domain gives

(20)

Applying the integration by parts for the left-hand side yields

(21)

Rewriting the second part of the left-hand side yields

(22)

where we can see that the boundary condition Eq. (9) could be easily incorporated into the weak expression.

Advantages and Disadvantages of the Curl Element

We have shown that by using the curl elements, the boundary conditions of Maxwell’s equations can be handled naturally. The curl elements enforce the tangential electric field to be continuous and allow the normal electric field to jump across the boundaries. Moreover, it also makes it easier to constrain other boundary conditions (Ref. 4).

For example, in the Electromagnetic Waves, Frequency Domain interface, the Perfect Electric Conductor boundary feature is set as the default to model electrically conducting surfaces, such as metals. The boundary condition enforces the tangential electric field to be zero; i.e., . In the Magnetic Fields interface, the default boundary condition is Magnetic Insulation, which constrains the tangential magnetic vector potential to be zero; i.e., . These boundary conditions could be easily considered by the FEM using pointwise constraints since the unknowns are exactly the tangential fields on the boundary. There are other advantages of using curl elements, such as eliminating spurious solutions, especially for solving electromagnetic wave problems (Ref. 5). However, the natural handling of the boundary conditions should be predominant.

There are a few disadvantages of using curl elements. For example, the linear curl element has local approximation errors of the order , where  is the element size, while using linear Lagrange elements, the local errors converge at  (Ref. 6). This is because the curl element is a mixed element where the order of the shape function varies in different directions. For instance, the tangential components of shape function  along edge  and any direction parallel to edge  are constants, although it is a linear function in other directions. The mixed property can also be shown by looking at the component, for example,

(23)

where  are constants depending on the coordinates of the element only.

The  component of  is constant along the  axis and is linear along the  axis. The accuracy of the spatial derivatives of each component would be significantly different. For this reason, when postprocessing curl elements, the higher-order spatial derivatives of the fields are not available. Equation (23) also shows that the shape function of the linear curl element can be constant along a specific direction. This makes the local error converge slower than that using a linear Lagrange element. On one hand, this disadvantage can be eliminated by using higher-order curl elements or finer meshes. On the other hand, compared to the advantages of handling boundary conditions naturally, the disadvantages become much less important, since the difficulties encountered by using Lagrange elements to solve equation (12) cannot be compensated by using higher-order shape functions or refining the mesh.

Summary

In this blog post, starting with Maxwell’s equations and their boundary conditions, we have introduced two basic types of equations that often appear in electromagnetics modeling; i.e., the scalar Poisson’s equation and the vector equation with  operator. We have shown that by using the classical Lagrange element to solve Poisson’s equation, the condition of continuous tangential electric fields is satisfied naturally. However, it is not suitable to use the Lagrange element to solve the vector equation due to the difficulties in handling the associated boundary conditions.

We then introduced the curl element, which could satisfy the condition of continuous tangential electric fields naturally. At the same time, we also have shown, by deriving the weak expressions in detail, how other boundary conditions are incorporated in FEM. As last, we talked about some disadvantages of using curl elements, which are much less important than the advantages.

References

1. H. Whitney, Geometric integration theory, Princeton UP, Princeton, 1957.
2. A. Nentchev, Numerical analysis and simulation in microelectronics by vector finite elements, 2008.
3. J.C. Nédélec, Mixed finite elements in ℝ³ . Numerische Mathematik, 35(3), pp. 315–341, 1980.
4. J.P. Webb, Edge elements and what they can do for you. IEEE Transactions on Magnetics, 29(2), pp.1460–1465, 1993.
5. J.M. Jin, Theory and computation of electromagnetic fields. John Wiley & Sons, 2011.
6. G. Mur, Edge elements, their advantages and their disadvantages. IEEE transactions on magnetics, 30(5), pp.3552–3557, 1994.

Performing lens simulations in wave optics is generally difficult, because it requires a lot of mesh elements. In this blog post, we demonstrate how the Wave Optics Module, an add-on to the COMSOL Multiphysics® software, can be used to perform lens simulations based on Maxwell’s equations.

Introduction to the Optics Simulation Methods

There are two main categories of methods to simulate optics:

1. Ray tracing
2. Wave optics

If you want to simulate the diffraction effect (even simply focusing a beam introduces diffraction), wave optics is needed. In wave optics, we consider two types of methods: a full-wave Maxwell method and a beam propagation method (BPM). Each method has certain limitations, outlined below:

Ray tracing is an approximation where the wavelength is negligible compared to the object size; therefore, it doesn’t deal with diffraction. The full-wave Maxwell solver literally solves Maxwell’s equations, so it’s rigorous and there is theoretically no model approximation. The BPM typically includes various approximations in the formulation, such as the Fraunhofer approximation (i.e., Fourier transformation) and the Fresnel diffraction formula.

The full-wave Maxwell solver looks like the greatest method. However, when it comes to optics simulation, there is a problem with the “conventional” Maxwell solver: It requires a fine mesh and lot of memory to solve:

• Optical components
• Interference patterns due to surface reflections

In the conventional Maxwell solver, all points within the computational domain contribute when running the simulation. For this reason, we need a mesh throughout the domain, and the mesh elements need to resolve the wavelength. Then, it becomes problematic when you want to simulate a large object, like standard optical lenses. The BPM doesn’t have this problem, because the field solution literally propagates (or jumps) from one plane to another by using a certain propagation law, in which you don’t need a mesh between the planes.

Lens Simulations with the Beam Envelopes Interface

Compared to conventional Maxwell solvers, the Beam Envelopes interface in the COMSOL® software doesn’t have this difficulty, because the fast oscillation part is factored out in the formulation. You can use this interface if the solution’s envelopes are slowly varying. In practice, there are many such cases. Using this method, you don’t need a lot of mesh elements. So, if we always simulate homogeneous domains and solve for a solution that has slowly varying envelopes, then we are done with this interface. But that’s not all…

We frequently want to solve optical systems that include inhomogeneous domains. The problem we face is the reflection from a material interface; a lens surface, for example. In which way do reflections create a problem? Reflections are also solutions to Maxwell’s equations. So, the Maxwell solver tries to find a solution including reflections if there are some material interfaces. If any reflections occur, they may constructively interfere with the incident beam ending up with standing waves with a half of the wavelength. This worsens the original problem. We need to resolve the half wavelength, which means many more mesh elements! This reduces the value of the Beam Envelopes interface. This situation is shown in the figure below.

A closeup of a lens simulation with the Beam Envelopes interface. There is interference in the lens (center part), which requires finer mesh.

To avoid the surface reflection, we can consider an antireflection (AR) coating, just as each optic has an AR coating in most cases in practice. Let’s take a look at an example of a Gaussian beam that propagates in a free air space, using the Gaussian Beam feature with the Matched boundary condition.

Top: The mesh used in the simulation. Only one mesh element is needed along the propagation direction (from left to right). Bottom: The Gaussian beam simulation with the Beam Envelopes interface, the unidirectional formulation. No material other than the air is inserted.

In the above simulation, we put the focus on the left boundary so the beam expands toward the right boundary. All other boundaries besides the left boundary are set to the Matched boundary condition with no excitation. Next, let’s add a glass on the right side of the domain. We expect a reflection in the left side of the domain and no reflection in the right side, so we have to increase the mesh in the left side, but we can keep the single mesh in the right side. (Note that you can still capture the reflection accurately with only one mesh element by using the bidirectional formulation. We are not interested in reflection here, so we stick with the unidirectional formulation.)

The Gaussian beam simulation with the Beam Envelopes interface, the unidirectional formulation. A glass is inserted in the right part of the domain. Shown above is the mesh. Many mesh elements are needed to resolve the half wavelength of the interference pattern, whereas only one mesh is needed in the right side of the domain.

As expected, we get a reflection in the left side of the domain, so we need a lot of mesh elements there. This hurts the advantage of the Beam Envelopes interface. Now, let’s add an AR coating on the glass surface. The simplest AR coating for a monochromatic light is the quarter-lambda AR coating (refer to Optics by Hecht). The quarter-lambda AR coating is a thin film with the refractive index of , where and are the index for each material sandwiching the film and with the thickness of , where is the vacuum wavelength. With this film, the reflectance becomes zero at . Let’s now see how we can include the AR coating in the simulation.

The Gaussian beam simulation with the Beam Envelopes interface, the unidirectional formulation. A glass is inserted in the right part of the domain. A quarter-lambda AR coating is put on the glass surface. Shown above is the mesh. Only one mesh is needed for all material domains.

Thanks to the AR coating, there is no longer any reflection, which gives the maximum benefit from this interface. We only need one mesh element in the propagating direction for each domain representing air, AR coating, and glass, respectively.

A boundary condition, introduced as of COMSOL Multiphysics version 5.4, the Transition boundary condition, mimics this quarter-lambda AR coating with zero thickness. All you need to do is to specify the refractive index and the thickness of the coating, which are and , as in the below figure.

Settings of the Transition boundary condition.

The Gaussian beam simulation with the Beam Envelopes interface, the unidirectional formulation. A glass is inserted in the right part of the domain. The Transition boundary condition is applied to the glass surface. Shown above is the mesh. Only one mesh is needed for all domains, since there are no reflections.

Now you can see how the Transition boundary condition is useful, particularly when there are many material interfaces, where you can avoid making a real thin-film coating on each surface.

Finally, with this boundary condition, the first figure of the lens simulation with a lot of interference becomes completely clean, as shown below.

A lens simulation with the Beam Envelopes interface, the unidirectional formulation, and the Transition boundary condition. There is no reflection causing interference, which enables a coarser mesh.

Concluding Remarks

Conventional full-wave Maxwell solvers require a lot of mesh elements when used for optics simulation. The Beam Envelopes interface, the unidirectional formulation, and the Transition boundary condition together address this problem under certain conditions. We can use this approach for large optical systems that include optics and even for multioptical systems couplings. Such applications include lens systems, waveguides, external optical systems, fiber couplings, laser diode stacks, and laser beam delivery systems.

Simulation of a waveguide that out-couples to the ambient air.

Next Step

See how the Wave Optics Module can benefit your lens simulations by clicking the button below: